
【题目】如图,在平行四边形ABCD中,对角线AC,BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动,若AC=12,BD=8,则经过________秒后,四边形BEDF是矩形.

【答案】2或8
【解析】
设经过t秒后,四边形BPDE是矩形;由平行四边形的性质得出OA=OC=![]() AC=6,OB=OD=
AC=6,OB=OD=![]() BD=4,得出OE=OF,证出四边形BFDE是平行四边形,当EF=BD,即OE=OD时,四边形BFDE是矩形,得出6-t=4,或t-6=2,解方程即可.
BD=4,得出OE=OF,证出四边形BFDE是平行四边形,当EF=BD,即OE=OD时,四边形BFDE是矩形,得出6-t=4,或t-6=2,解方程即可.
解:设经过t秒后,四边形BPDQ是矩形;
则AE=CF=t,
∵四边形ABCD是平行四边形,
∴OA=OC=![]() AC=6,OB=OD=
AC=6,OB=OD=![]() BD=4,
BD=4,
∴OE=OF,
∴四边形BFDE是平行四边形,
当EF=BD,即OE=OD时,四边形BFDE是矩形,
此时6-t=4,或t-6=2,
解得:t=2,或t=8,
即经过2秒或8秒后,四边形BPDE是矩形.
故答案为: 2或8.


科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(﹣1)2018+3﹣2﹣(π﹣3.14)0
(2)(x+3)2﹣x2
(3)(x+2)(3x﹣y)﹣3x(x+y)
(4)(2x+y+1)(2x+y﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=90 , BC=12,tanC=![]() . 如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且
. 如果一质点P开始时在AB边的P0处,BP0=3.P第一步从P0跳到AC边的P1(第1次落点)处,且![]() ;第二步从P1跳到BC边的P2(第2次落点)处,且
;第二步从P1跳到BC边的P2(第2次落点)处,且![]() ;第三步从P2跳到AB边的P3(第3次落点)处,且
;第三步从P2跳到AB边的P3(第3次落点)处,且![]() ;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
;…;质点P按照上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2014与点P2015之间的距离为( )
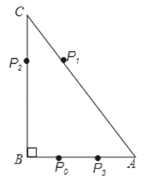
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例反数y=![]() (x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=
(x>0)的图象如图所示,点B在图象上,连接OB并延长到点A,使AB=OB,过点A作AC∥y轴交y=![]() (x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=________.
(x>0)的图象于点C,连接BC、OC,S△BOC=3,则k=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中:①等腰三角形底边的中点到两腰的距离相等;②等腰三角形的高、中线、角平分线互相重合;③若![]() 与
与![]() 成轴对称,则
成轴对称,则![]() 一定与
一定与![]() 全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
全等;④有一个角是60度的三角形是等边三角形;⑤等腰三角形的对称轴是顶角的平分线.正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成以下证明:
已知:点P在直线CD上,∠BAP+∠APD=180°,∠1=∠2.
求证:AB∥CD,∠E=∠F.
证明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性质)
∴AE∥PF.( )
∴∠E=∠F.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A、B分别在y轴的正半轴和x轴的正半轴上,OA=OB,△AOB的面积为18.过点A作直线l⊥y轴.
(1)求点A的坐标;
(2)点C是第一象限直线l上一动点,连接BC,过点B作BD⊥BC,交y轴于点设点D的纵坐标为t,点C的横坐标为d,求t与d的关系式;
(3)在(2)的条件下,过点D作直线DF∥AB,交x轴于点F,交直线l于点E,OF=![]() EC时,求点E的坐标.
EC时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com