
如图,将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF,∠ABC=α=60°,BF=AF.
(1)求证:DA∥BC;
(2)猜想线段DF、AF的数量关系,并证明你的猜想.
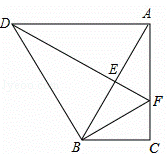
(1)证明:由旋转的性质可知:∠DBE=∠ABC=60°,BD=AB,
∴△ABD为等边三角形,
∴∠DAB=60°,
∴∠DAB=∠ABC,
∴DA∥BC;
(2)猜想:DF=2AF,
证明如下:如图,在DF上截取DG=AF,连接BG,
由旋转的性质可知,DB=AB,∠BDG=∠BAF,
在△DBG和△ABF中,
 ,
,
∴△DBG≌△ABF(SAS),
∴BG=BF,∠DBG=∠ABF,
∵∠DBG+∠GBE=α=60°,
∴∠GBE+∠ABF=60°,即∠GBF=α=60°,
又∵BG=BF,
∴△BGF为等边三角形,
∴GF=BF,
又∵BF=AF,
∴FG=AF,
∴DF=DG+FG=AF+AF=2AF.



科目:初中数学 来源: 题型:
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(s in25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
in25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,P点关于原点的对称点为P1(﹣3,﹣ ),P点关于x轴的对称点为P2(a,b),则
),P点关于x轴的对称点为P2(a,b),则 =( )
=( )
A. ﹣2 B2 C. 4 D. ﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠C=90°, ,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么
,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么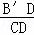 = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
推理证明:如图1,在正方形ABCD和正方形CGFE中,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,求证:S1=S2.
猜想论证:如图2,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1、S2的数量关系,并加以证明.
拓展探究:如图3,在△ABC中,AB=AC=10cm,∠B=30°,把△ABC沿AC翻折到△ACE,过点A作AD∥CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请你直接写出CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
A. 6条 B.7条 C. 8条 D. 9条
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中,错误的是( )
A. 平行四边形的对角线互相平分
B. 菱形的对角线互相垂直平分
C.  矩形的对角线相等且互相垂直平分
矩形的对角线相等且互相垂直平分
D. 角平分线上的点到角两边的距离相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com