
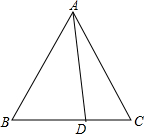
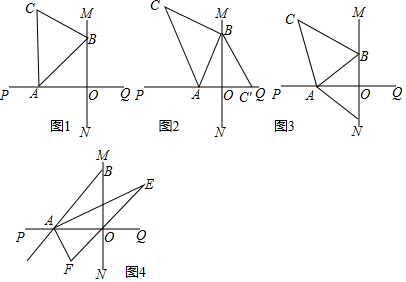
 如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.
如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由. 分析 如图在AD上取一点F,用量角器使得∠BFD=60°,延长BF交AC于E,则AE=CD.
解答 解: 如图在AD上取一点F,用量角器使得∠BFD=60°,延长BF交AC于E,则AE=CD.
如图在AD上取一点F,用量角器使得∠BFD=60°,延长BF交AC于E,则AE=CD.
理由如下:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠C=60°,
∵∠BFD=∠FBA+∠BAF=60°,∠BAF+∠DAC=60°,
∴∠ABE=∠CAD,
在△ABE和△CAD中,
$\left\{\begin{array}{l}{∠ABE=∠CAD}\\{AB=AC}\\{∠BAE=∠C}\end{array}\right.$,
∴△ABE≌△CAD,
∴AE=CD.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是熟练掌握基本题型,学会添加常用辅助线构造全等三角形解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
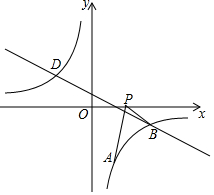 如图,已知点A(1,a)是反比例函数y=-$\frac{3}{x}$的图象上一点,直线y=-$\frac{1}{2}x+\frac{1}{2}$与反比例函数y=-$\frac{3}{x}$的图象在第四象限的交点为点B.
如图,已知点A(1,a)是反比例函数y=-$\frac{3}{x}$的图象上一点,直线y=-$\frac{1}{2}x+\frac{1}{2}$与反比例函数y=-$\frac{3}{x}$的图象在第四象限的交点为点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
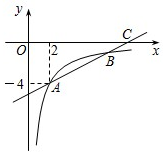 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
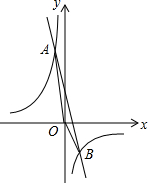 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
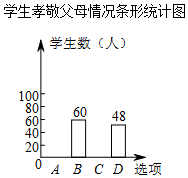 某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:
某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其它),在全校范围内随机抽取了若干名学生进行调查,得到如图表(部分信息未给出):根据以上信息解答下列问题:| 选项 | 频数 | 频率 |
| A | m | 0.15 |
| B | 60 | p |
| C | n | 0.4 |
| D | 48 | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com