
 如图,OA⊥OB,OD、OE分别是∠AOC、∠BOC的平分线,则∠DOE=45度.
如图,OA⊥OB,OD、OE分别是∠AOC、∠BOC的平分线,则∠DOE=45度. 分析 首先根据垂线定义可得∠AOB=90°,再根据角平分线定义可得∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠COB,进而可得答案.
解答 解:∵OA⊥OB,
∴∠AOB=90°,
∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠COB,
∴∠DOE=∠EOC+∠COD=$\frac{1}{2}∠BOC+\frac{1}{2}∠AOC$=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}×90°$=45°,
故答案为:45.
点评 此题主要考查了垂线,以及角平分线定义,关键是掌握角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.


科目:初中数学 来源: 题型:解答题
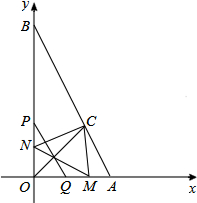 如图,在平面直角坐标系中,点A(2,0)、B(0,4),∠AOB的平分线交AB于点C,动点P从点O出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,PQ∥AB,交x轴于点Q,过点P、Q作关于直线OC的对称点M,N,连接MC、NC、MN,设点P运动的时间为t(0<t<2).
如图,在平面直角坐标系中,点A(2,0)、B(0,4),∠AOB的平分线交AB于点C,动点P从点O出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,PQ∥AB,交x轴于点Q,过点P、Q作关于直线OC的对称点M,N,连接MC、NC、MN,设点P运动的时间为t(0<t<2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{-a-b}$ | B. | $\frac{a}{a+b}$ | C. | $\frac{a}{-a+b}$ | D. | $\frac{a}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点确定一条直线 | B. | 两点之间直线最短 | ||
| C. | 两点之间线段最短 | D. | 直线比曲线短 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
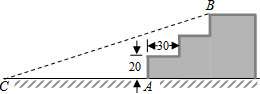 如图,某地入口处原有三级台阶,每级台阶高为20cm,深为30
如图,某地入口处原有三级台阶,每级台阶高为20cm,深为30| A. | 200cm | B. | 210cm | C. | 240cm | D. | 300cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
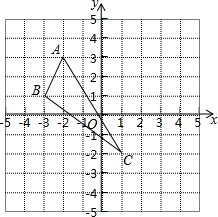 (1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com