Question

已知矩形的两对角线所夹的角为60°，且其中一条对角线长为4cm，则该矩形的两边长分别为________cm，________cm．

Answer 1

2    
分析：矩形的两对角线所夹的角为60°，加上矩形的性质可得到△AOB的形状为等边三角形，进而根据已知线段AC，求得对角线的一半长，那么可得到AB长，根据勾股定理可得到BC长．
解答：解：如图：∵四边形为矩形，∠DOC=60°，BD=AC=4cm，
∴OD=OC=AC=×4=2cm，
又∵∠DOC=60°，
∴△DOC是等边三角形，CD=OD=2cm，
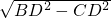
在直角△DBC中，BD=4cm，CD=2cm，根据勾股定理BC===2cm．
故答案为2．
点评：矩形的两对角线所夹的角为60°，那么对角线的一边和两条对角线的一半组成等边三角形．综合考查了矩形的性质及勾股定理的运用．