
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
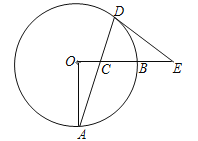
(1)求证:∠ECD=∠EDC;
(2)若tanA=![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
【答案】(1)证明见解析;
(2)DE的长为15;
(3)弦AD在圆内扫过的面积为![]()
【解析】试题分析:(1)连结OD,已知DE是⊙O的切线,根据切线的性质可得∠EDC+∠ODA=90°,已知 OA⊥OB,可得∠ACO+∠A=90°,因OA=OD,根据等腰三角形的性质可得∠ODA=∠A,即可得∠EDC=∠ACO,因∠ECD=∠ACO,即可得∠ECD=∠EDC.(2)因为tanA=![]() ,即可得
,即可得![]() ,求得OC=2, 设DE=x,可得CE=x,所以OE=2+x,在Rt△ODE中,根据勾股定理可得OD2+DE2=OE2, 即可得82+x 2=(2+x)2,解得x=15,所以DE=CE=15. (3)过点D作AO的垂线,交AO的延长于F,当
,求得OC=2, 设DE=x,可得CE=x,所以OE=2+x,在Rt△ODE中,根据勾股定理可得OD2+DE2=OE2, 即可得82+x 2=(2+x)2,解得x=15,所以DE=CE=15. (3)过点D作AO的垂线,交AO的延长于F,当![]() 时,
时, ![]() ,DF=4,求得
,DF=4,求得![]() 的面积,当
的面积,当![]() 时,
时, ![]() ,DF=4
,DF=4![]() ,求得
,求得![]() ,即可求得弦AD在圆内扫过的面积.
,即可求得弦AD在圆内扫过的面积.
试题解析:
(1)证明:连结OD,
∵DE是⊙O的切线,∴∠EDC+∠ODA=900,
又∵OA⊥OB,∴∠ACO+∠A=900,
∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO,
又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA=![]() ,∴
,∴![]() ,∴OC=2,
,∴OC=2,
设DE=x,∵∠ECD=∠EDC,∴CE=x,∴OE=2+x.
∴∠ODE=900,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
(3)解:过点D作AO的垂线,交AO的延长于F,
当![]() 时,
时, ![]() ,DF=4,
,DF=4,
![]()
当![]() 时,
时, ![]() ,DF=4
,DF=4![]() ,
,
![]() ,
,
![]()
![]()
![]()


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的10×5网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点B按下列步骤移动第一步:点B绕点A逆时针旋转180°得到点B1;第二步:点B1绕点D逆时针旋转90°得到点B2;第三步:点B2绕点C逆时针旋转90°回到点B
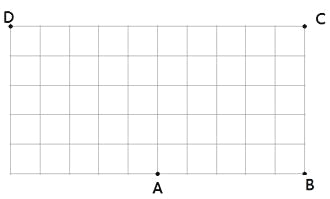
(1)请用圆规画出点B→B1→B2→B经过的路径;
(2)所画图形是_______图形;
(3)求所画图形的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜店第一次用400元购进某种蔬菜,由于销售状况良好,该店又用700元第二次购进该品种蔬菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有2% 的损耗,第二次购进的蔬菜有3% 的损耗,若该蔬菜店售完这些蔬菜获利不低于944元,则该蔬菜每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 为斜边分别向外侧作等腰直角三角形,直角顶点分别为
为斜边分别向外侧作等腰直角三角形,直角顶点分别为![]() 、
、![]() 、
、![]() 、
、![]() ,顺次连结这四个点,得四边形
,顺次连结这四个点,得四边形![]() .
.
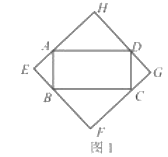
(1)如图1,当四边形![]() 为矩形时,请判断四边形
为矩形时,请判断四边形![]() 的形状(不要求证明).
的形状(不要求证明).
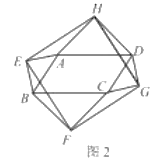
(2)如图2,当四边形![]() 为一般平行四边形时,设
为一般平行四边形时,设![]()
①试用含![]() 的代数式表示
的代数式表示![]() ,写出解答过程;
,写出解答过程;
②求证:![]() ,并判断四边形
,并判断四边形![]() 是什么四边形?请说明理由.
是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
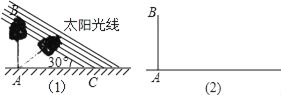
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有![]() 个大小、质地都相同的乒乓球,球面上分别标有数字
个大小、质地都相同的乒乓球,球面上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,搅匀后先从中摸出一个球(不放回),再从余下的
,搅匀后先从中摸出一个球(不放回),再从余下的![]() 个球中摸出
个球中摸出![]() 个球.
个球.
(1)用树状图列出所有可能出现的结果;
(2)求![]() 次摸出的乒乓球球面上数字的积为偶数的概率.
次摸出的乒乓球球面上数字的积为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,当x=1时,y=1;当x=-2时,y=-14.
(1)求这个一次函数的关系式;
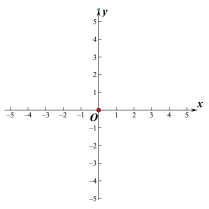
(2)在如图所示的平面直角坐标系中作出函数的图像;
(3)由图像观察,当0≤x≤2时,函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
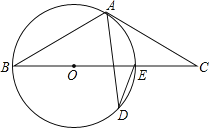
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com