
【题目】抛物线y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
与x轴交于点A,B(点A在点B的左边),与y轴交于点C,点D是该抛物线的顶点.
(1)如图1,连接CD,求线段CD的长;
(2)如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F,PF与线段AC交于点E;将线段OB沿x轴左右平移,线段OB的对应线段是O1B1,当PE+![]() EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
EC的值最大时,求四边形PO1B1C周长的最小值,并求出对应的点O1的坐标;
(3)如图3,点H是线段AB的中点,连接CH,将△OBC沿直线CH翻折至△O2B2C的位置,再将△O2B2C绕点B2旋转一周在旋转过程中,点O2,C的对应点分别是点O3,C1,直线O3C1分别与直线AC,x轴交于点M,N.那么,在△O2B2C的整个旋转过程中,是否存在恰当的位置,使△AMN是以MN为腰的等腰三角形?若存在,请直接写出所有符合条件的线段O2M的长;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() (3),O2M的长
(3),O2M的长![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)分别表示C和D的坐标,利用勾股定理可得CD的长;
(2)令y=0,可求得A(-3![]() ,0),B(
,0),B(![]() ,0),利用待定系数法可计算直线AC的解析式为:y=
,0),利用待定系数法可计算直线AC的解析式为:y=![]() x+
x+![]() ,设E(x,
,设E(x,![]() x+
x+![]() ),P(x,﹣
),P(x,﹣![]() x2﹣
x2﹣![]() x+
x+![]() ),表示PE的长,利用勾股定理计算AC的长,发现∠CAO=30°,得AE=2EF=
),表示PE的长,利用勾股定理计算AC的长,发现∠CAO=30°,得AE=2EF=![]() x+2
x+2![]() ,计算PE+
,计算PE+![]() EC,利用配方法可得当PE+
EC,利用配方法可得当PE+![]() EC的值最大时,x=-2
EC的值最大时,x=-2![]() ,此时P(-2
,此时P(-2![]() ,
,![]() ),确定要使四边形PO1B1C周长的最小,即PO1+B1C的值最小,将点P向右平移
),确定要使四边形PO1B1C周长的最小,即PO1+B1C的值最小,将点P向右平移![]() 个单位长度得点P1(-
个单位长度得点P1(-![]() ,
,![]() ),连接P1B1,则PO1=P1B1,再作点P1关于x轴的对称点P2(-
),连接P1B1,则PO1=P1B1,再作点P1关于x轴的对称点P2(-![]() ,-
,-![]() ),可得结论;
),可得结论;
(3)先确定对折后O2C落在AC上,△AMN是以MN为腰的等腰三角形存在四种情况:
①如图4,AN=MN,证明△C1EC≌△B2O2M,可计算O2M的长;
②如图5,AM=MN,此时M与C重合,O2M=O2C=![]() ;
;
③如图6,AM=MN,N和H、C1重合,可得结论;
④如图7,AN=MN,过C1作C1E⊥AC于E证明四边形C1EO2B2是矩形,根据O2M=EO2+EM可得结论.
(1)如图1,过点D作DK⊥y轴于K,

当x=0时,y=![]() ,
,
∴C(0,![]() ),
),
y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() =-
=-![]() ,
,
∴D(-![]() ,
,![]() ),
),
∴DK=![]() ,CK=
,CK=![]() -
-![]() =
=![]() ,
,
∴CD=![]() ;
;
(2)在y=-![]() x2﹣
x2﹣![]() x+
x+![]() 中,令y=0,则-
中,令y=0,则-![]() x2﹣
x2﹣![]() x+
x+![]() =0,
=0,
解得:x1=-3![]() ,x2=
,x2=![]() ,
,
∴A(-3![]() ,0),B(
,0),B(![]() ,0),
,0),
∵C(0,![]() ),
),
易得直线AC的解析式为:y=![]() x+
x+![]() ,
,
设E(x,![]() x+
x+![]() ),P(x,-
),P(x,-![]() x2﹣
x2﹣![]() x+
x+![]() ),
),
∴PF=-![]() x2﹣
x2﹣![]() x+
x+![]() ,EF=
,EF=![]() x+
x+![]() ,
,
Rt△ACO中,AO=3![]() ,OC=
,OC=![]() ,
,
∴AC=2![]() ,
,
∴∠CAO=30°,
∴AE=2EF=![]() x+
x+![]() ,
,
∴PE+![]() EC=(-
EC=(-![]() x2﹣
x2﹣![]() x+
x+![]() )-(
)-(![]() x+
x+![]() )+
)+![]() (AC-AE),
(AC-AE),
=-![]() x2-
x2-![]() x+
x+![]() [2
[2![]() -(
-(![]() x+
x+![]() )],
)],
=-![]() x2-
x2-![]() x-
x-![]() x,
x,
=-![]() (x+2
(x+2![]() )2+
)2+![]() ,
,
∴当PE+![]() EC的值最大时,x=-2
EC的值最大时,x=-2![]() ,此时P(-2
,此时P(-2![]() ,
,![]() ),
),
∴PC=2![]() ,
,
∵O1B1=OB=![]() ,
,
∴要使四边形PO1B1C周长的最小,即PO1+B1C的值最小,
如图2,将点P向右平移![]() 个单位长度得点P1(-
个单位长度得点P1(-![]() ,
,![]() ),连接P1B1,则PO1=P1B1,
),连接P1B1,则PO1=P1B1,

再作点P1关于x轴的对称点P2(-![]() ,-
,-![]() ),则P1B1=P2B1,
),则P1B1=P2B1,
∴PO1+B1C=P2B1+B1C,
∴连接P2C与x轴的交点即为使PO1+B1C的值最小时的点B1,
∴B1(-![]() ,0),
,0),
将B1向左平移![]() 个单位长度即得点O1,
个单位长度即得点O1,
此时PO1+B1C=P2C=![]() ,
,
对应的点O1的坐标为(-![]() ,0),
,0),
∴四边形PO1B1C周长的最小值为![]() ;
;
(3)O2M的长度为![]() 或
或![]() 或2
或2![]() +
+![]() 或2
或2![]() -
-![]() .
.
理由是:如图3,
∵H是AB的中点,
∴OH=![]() ,
,
∵OC=![]() ,
,
∴CH=BC=2![]() ,
,
∴∠HCO=∠BCO=30°,
∵∠ACO=60°,
∴将CO沿CH对折后落在直线AC上,即O2在AC上,
∴∠B2CA=∠CAB=30°,
∴B2C∥AB,
∴B2(-2![]() ,
,![]() ),
),
①如图4,AN=MN,

∴∠MAN=∠AMN=30°=∠O2B2O3,
由旋转得:∠CB2C1=∠O2B2O3=30°,B2C=B2C1,
∴∠B2CC1=∠B2C1C=75°,
过C1作C1E⊥B2C于E,
∵B2C=B2C1=2![]() ,
,
∴C1E=![]() =B2O2,B2E=
=B2O2,B2E=![]() ,
,
∵∠O2MB2=∠B2MO3=75°=∠B2CC1,
∠B2O2M=∠C1EC=90°,
∴△C1EC≌△B2O2M,
∴O2M=CE=B2C-B2E=2![]() -
-![]() ;
;
②如图5,AM=MN,此时M与C重合,O2M=O2C=![]() ,
,

③如图6,AM=MN,

∵B2C=B2C1=2![]() =B2H,即N和H、C1重合,
=B2H,即N和H、C1重合,
∴∠CAO=∠AHM=∠MHO2=30°,
∴O2M=![]() AO2=
AO2=![]() ;
;
④如图7,AN=MN,过C1作C1E⊥AC于E,

∴∠NMA=∠NAM=30°,
∵∠O3C1B2=30°=∠O3MA,
∴C1B2∥AC,
∴∠C1B2O2=∠AO2B2=90°,
∵∠C1EC=90°,
∴四边形C1EO2B2是矩形,
∴EO2=C1B2=2![]() ,C1E=B2O2=
,C1E=B2O2=![]() ,
,
∴EM=![]() ,
,
∴O2M=EO2+EM=2![]() +
+![]() ,
,
综上所述,O2M的长是![]() 或
或![]() 或2
或2![]() +
+![]() 或2
或2![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图, A为x轴负半轴上一点, B为x轴正半轴上一点, C(0,-2),D(-3,-2).
(1)求△BCD的面积;
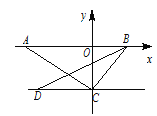
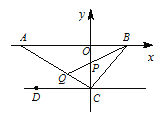
(2)若AC⊥BC,作∠CBA的平分线交CO于P,交CA于Q,判断∠CPQ与∠CQP的大小关系, 并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
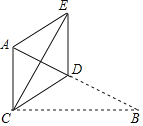
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
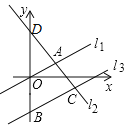
【题目】如图,在平面直角坐标系中,直线l1:y=![]() x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为﹣2.直线l2与y轴交于点D.
x与直线l2交点A的横坐标为2,将直线l1沿y轴向下平移4个单位长度,得到直线l3,直线l3与y轴交于点B,与直线l2交于点C,点C的纵坐标为﹣2.直线l2与y轴交于点D.
(1)求直线l2的解析式;
(2)求△BDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017辽宁省葫芦岛市)如图,∠MAN=60°,AP平分∠MAN,点B是射线AP上一定点,点C在直线AN上运动,连接BC,将∠ABC(0°<∠ABC<120°)的两边射线BC和BA分别绕点B顺时针旋转120°,旋转后角的两边分别与射线AM交于点D和点E.
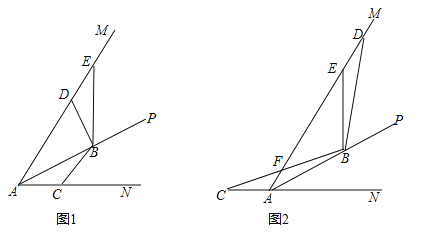
(1)如图1,当点C在射线AN上时,①请判断线段BC与BD的数量关系,直接写出结论;
②请探究线段AC,AD和BE之间的数量关系,写出结论并证明;
(2)如图2,当点C在射线AN的反向延长线上时,BC交射线AM于点F,若AB=4,AC=![]() ,请直接写出线段AD和DF的长.
,请直接写出线段AD和DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com