
،¾جâؤ؟،؟ثو×إ³اتذ»¯½¨ةèµؤ·¢ص¹£¬½»ح¨سµ¶آ³ةخھةد°à¸ك·هت±ؤرزش±ـأâµؤدضدَ£®خھءث½âءْبھونؤ³جُµہآ·½»ح¨سµ¶آاé؟ِ£¬ءْبھؤ³ضذر§ح¬ر§¾تµµطح³¼ئ·ضخِرذ¾؟±يأ÷£؛µ±![]() ت±£¬³µء÷ثظ¶بv£¨ا§أ×/ذ،ت±£©تا³µء÷أـ¶بx£¨ء¾/ا§أ×£©µؤز»´خ؛¯ت£®µ±¸أµہآ·µؤ³µء÷أـ¶ب´ïµ½220ء¾/ا§أ×ت±£¬شى³ة¶آبû£¬´ثت±³µء÷ثظ¶بخھ0ا§أ×/ذ،ت±£»µ±³µء÷أـ¶بخھ95ء¾/ا§أ×ت±£¬³µء÷ثظ¶بخھ50ا§أ×/ذ،ت±£®
ت±£¬³µء÷ثظ¶بv£¨ا§أ×/ذ،ت±£©تا³µء÷أـ¶بx£¨ء¾/ا§أ×£©µؤز»´خ؛¯ت£®µ±¸أµہآ·µؤ³µء÷أـ¶ب´ïµ½220ء¾/ا§أ×ت±£¬شى³ة¶آبû£¬´ثت±³µء÷ثظ¶بخھ0ا§أ×/ذ،ت±£»µ±³µء÷أـ¶بخھ95ء¾/ا§أ×ت±£¬³µء÷ثظ¶بخھ50ا§أ×/ذ،ت±£®
£¨1£©µ±![]() ت±£¬اَ³µء÷ثظ¶بv£¨ا§أ×/ذ،ت±£©سë³µء÷أـ¶بx£¨ء¾/ا§أ×£©µؤ؛¯ت¹طدµت½£»
ت±£¬اَ³µء÷ثظ¶بv£¨ا§أ×/ذ،ت±£©سë³µء÷أـ¶بx£¨ء¾/ا§أ×£©µؤ؛¯ت¹طدµت½£»
£¨2£©خھت¹¸أµہآ·ةد³µء÷ثظ¶ب´َسع40ا§أ×/ذ،ت±ازذ،سع60ا§أ×/ذ،ت±£¬س¦؟طضئ¸أµہآ·ةدµؤ³µء÷أـ¶بشعت²أ´·¶خ§ؤع£؟
£¨3£©³µء÷ء؟£¨ء¾/ذ،ت±£©تاµ¥خ»ت±¼نؤعح¨¹¸أµہآ·ةدؤ³¹غ²âµمµؤ³µء¾ت£¬¼´£؛³µء÷ء؟=³µء÷ثظ¶ب،ء³µء÷أـ¶ب£®µ±![]() ت±£¬اَ¸أµہآ·ةد³µء÷ء؟yµؤ×î´َضµ£®´ثت±³µء÷ثظ¶بخھ¶àةظ£؟
ت±£¬اَ¸أµہآ·ةد³µء÷ء؟yµؤ×î´َضµ£®´ثت±³µء÷ثظ¶بخھ¶àةظ£؟
،¾´ً°¸،؟£¨1£©v£½©پ![]() x+88£»£¨2£©70£¼x£¼120£»£¨3£©³µء÷ء؟yµؤ×î´َضµتاأ؟ذ،ت±4840ء¾£¬´ثت±³µء÷ثظ¶بتا44ا§أ×/ت±£®
x+88£»£¨2£©70£¼x£¼120£»£¨3£©³µء÷ء؟yµؤ×î´َضµتاأ؟ذ،ت±4840ء¾£¬´ثت±³µء÷ثظ¶بتا44ا§أ×/ت±£®
،¾½âخِ،؟
£¨1£©µ±20،ـx،ـ220ت±£¬ةè³µء÷ثظ¶بvسë³µء÷أـ¶بxµؤ؛¯ت¹طدµت½خھv£½kx+b£¬شظ¸ù¾ف´¶¨دµت·¨اَ½â¼´؟ة£»
£¨2£©سة£¨1£©µؤ½âخِت½½¨ء¢²»µبت½×éاَ³ِئن½â¼¯¼´؟ة£»
£¨3£©ةè³µء÷ء؟yسëxض®¼نµؤ¹طدµت½خھy£½vx£¬µ±20،ـx،ـ220ت±±يت¾³ِدàس¦µؤ¶´خ؛¯ت¹طدµ£¬سة¶´خ؛¯تµؤذشضت¾ح؟ةزشاَ³ِ½ل¹û£®
½â£؛£¨1£©ةè³µء÷ثظ¶بvسë³µء÷أـ¶بxµؤ؛¯ت¹طدµت½خھv£½kx+b£¬سةجâز⣬µأ
![]() £¬½âµأ£؛
£¬½âµأ£؛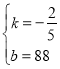 £¬
£¬
،൱20،ـx،ـ220ت±£¬v£½©پ![]() x+88£»
x+88£»
£¨2£©سةجâز⣬µأ£؛ £¬½âµأ£؛70£¼x£¼120£¬
£¬½âµأ£؛70£¼x£¼120£¬
،àس¦؟طضئ¸أµہآ·ةدµؤ³µء÷أـ¶بشع70£¼x£¼120·¶خ§ؤع£»
£¨3£©ةè³µء÷ء؟yسëxض®¼نµؤ¹طدµت½خھy£½vx£¬
µ±20،ـx،ـ220ت±£¬y£½£¨©پ![]() x+88£©x£½©پ
x+88£©x£½©پ![]() £¨x©پ110£©2+4840£¬
£¨x©پ110£©2+4840£¬
،൱x£½110ت±£¬y×î´َ£½4840£¬´ثت±![]() ا§أ×/ت±£¬
ا§أ×/ت±£¬
،൱³µء÷أـ¶بتا110ء¾/ا§أ×ت±£¬³µء÷ء؟yب،µأ×î´َضµتاأ؟ذ،ت±4840ء¾£¬´ثت±³µء÷ثظ¶بتا44ا§أ×/ت±£®


 ¶ل¹ع½ً¾يب«ؤـء·؟¼دµءذ´ً°¸
¶ل¹ع½ً¾يب«ؤـء·؟¼دµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعز»¸ِ²»ح¸أ÷µؤ؟ع´üہï×°سذض»سذرصة«²»ح¬µؤ؛ع،¢°×ء½ضضرصة«µؤاٍ¹²5ض»£®ؤ³ر§د°ذ،×é×ِأاٍتµر飬½«اٍ½ءشب؛َ´سضذثو»ْأ³ِز»¸ِاٍ¼ادآرصة«£¬شظ°رثü·إ»ط´üضذ£¬²»¶دضط¸´£®دآ±يتا»î¶¯½ّذذضذµؤز»×éح³¼ئت¾ف£؛
أاٍµؤ´خت n | 100 | 150 | 200 | 500 | 800 | 1000 |
أµ½°×اٍµؤ´خت m | 58 | 96 | 116 | 295 | 484 | 601 |
أµ½°×اٍµؤئµآت | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
£¨1£©اë¹ہ¼ئ£؛µ±n؛ـ´َت±£¬أµ½°×اٍµؤئµآت½«»ل½س½ü،، £¨½ل¹û¾«ب·µ½0.1£©£»
£¨2£©تش¹ہثم؟ع´üضذ؛عاٍسذ،، ض»£¬°×اٍسذ،، ض»£»
£¨3£©شع£¨2£©µؤ½لآغدآ£¬اëؤمسأءذ±ي»ٍت÷×´ح¼اَ³ِثو»ْأ³ِء½¸ِاٍ¶¼تا°×اٍµؤ¸إآت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬µمEتا±ك³¤خھ2µؤص·½ذخABCDµؤ±كBCةدµؤز»¶¯µم£¨²»سë¶ثµمضط؛د£©£¬½«،÷ABEرطAE·صغضء،÷AFEµؤخ»ضأ£¬بô،÷CDFتاµبرüب½اذخ£¬شٍBE=________£®
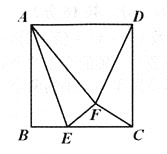
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³·×°µêµؤش±¹¤سëہد°هئëذؤذء¦£¬شع2019ؤêµؤ¾سھضذ£¬أ؟شآµؤہûبَ¶¼شع²»¶دشِ¼س.¸أ·×°µêµؤہد°هأ؟¼¾¶ب¶¼بأش±¹¤×ـ½ل¾رéسë²»×م£¬دآأوتا²ك»®ت¦سëدْتغ![]() ئ·إئ·×°µؤش±¹¤شعµع¶¼¾¶ب×ـ½لµؤز»²؟·ض.
ئ·إئ·×°µؤش±¹¤شعµع¶¼¾¶ب×ـ½لµؤز»²؟·ض.
²ك»®ت¦µؤ·¢رش£؛µعثؤشآµؤہûبَخھ50حٍشھ£¬´سµعثؤشآ؟ھت¼£¬µع¶¼¾¶بµؤشآشِ³¤آت²»±ن£¬µع¶¼¾¶بµؤ×ـہûبَخھ182حٍشھ.
دْتغ![]() ئ·إئµؤش±¹¤·¢رش£؛دْتغµؤ
ئ·إئµؤش±¹¤·¢رش£؛دْتغµؤ![]() ئ·إئ·×°شعثؤشآ·فضذ£¬½ّ¼غخھ100شھ£¬تغ¼غخھ140شھ£¬أ؟ضـدْتغ60¼£¬سةسع¸أ·×°½ّ»ُء؟ةظ£¬زٍ´ث£¬²ةسأصا¼غدْتغ£¬أ؟¼صا1شھت±£¬ئ½¾ùأ؟ضـةظتغ2¼£¬أ؟ضـس¯ہû2250شھ.
ئ·إئ·×°شعثؤشآ·فضذ£¬½ّ¼غخھ100شھ£¬تغ¼غخھ140شھ£¬أ؟ضـدْتغ60¼£¬سةسع¸أ·×°½ّ»ُء؟ةظ£¬زٍ´ث£¬²ةسأصا¼غدْتغ£¬أ؟¼صا1شھت±£¬ئ½¾ùأ؟ضـةظتغ2¼£¬أ؟ضـس¯ہû2250شھ.

اë¸ù¾ف×ـ½ل½â´ًدà¹طµؤختجâ£؛
£¨1£©اَµع¶¼¾¶بشآشِ³¤آت£»
£¨2£©![]() ئ·إئ·×°أ؟ضـس¯ہû2250شھت±£¬أ؟¼تغ¼غس¦¸أتا¶àةظشھ?
ئ·إئ·×°أ؟ضـس¯ہû2250شھت±£¬أ؟¼تغ¼غس¦¸أتا¶àةظشھ?
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
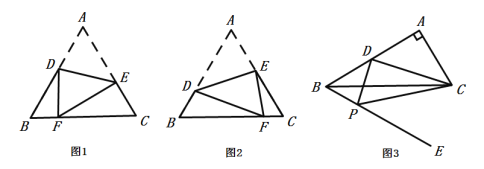
،¾جâؤ؟،؟£¨1£©بçح¼1£¬،÷ABCخھµب±كب½اذخ£¬µمD،¢E·ض±ًخھ±كAB،¢ACةدµؤز»µم£¬½«ح¼ذخرطدك¶خDEثùشعµؤض±دك·صغ£¬ت¹µمAآنشعBC±كةدµؤµمF´¦اَض¤£؛![]() £»
£»
£¨2£©بçح¼2£¬°´ح¼1µؤ·صغ·½ت½£¬بôµب±ك،÷ABCµؤ±ك³¤خھ4£¬µ±![]() ت±£¬اَ
ت±£¬اَ![]() µؤضµ£»
µؤضµ£»
£¨3£©بçح¼3£¬شع![]() ضذ£¬
ضذ£¬![]() £¬µمDتاAB±كةدµؤضذµم£¬شعBCµؤدآ·½×÷ةندكBE£¬ت¹µأ
£¬µمDتاAB±كةدµؤضذµم£¬شعBCµؤدآ·½×÷ةندكBE£¬ت¹µأ![]() £¬µمPتاةندكBEةدز»¸ِ¶¯µم£¬µ±
£¬µمPتاةندكBEةدز»¸ِ¶¯µم£¬µ±![]() £¬اَBPµؤ³¤.
£¬اَBPµؤ³¤.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھµمM£¨n£¬©پn £©شعµع¶دَدق£¬¹µمMµؤض±دكy=kx+b£¨0£¼k£¼1£©·ض±ً½»xضل،¢yضلسعµمA£¬B£¬¹µمM×÷MN،حxضلسعµمN£¬شٍدآءذµمشعدك¶خANµؤتا£¨،،،،£©
A. £¨£¨k©پ1£©n£¬0£© B. £¨£¨k+![]() £©n£¬0£©£© C. £¨
£©n£¬0£©£© C. £¨![]() £¬0£© D. £¨£¨k+1£©n£¬0£©
£¬0£© D. £¨£¨k+1£©n£¬0£©
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع¾طذخABCDضذ£¬Oتا¶ش½ادكACµؤضذµم£®½«ABCDبئµمBث³ت±صëذ×ھ90،م£®ذ×ھ؛َµؤثؤ±كذخخھA'B،نC،نD'£¬µمA£¬C£¬D£¬Oµؤ¶شس¦µم·ض±ًخھA،ن£¬C'£¬D'£¬O،¯£¬بôAB£½8£¬BC£½10£¬شٍدك¶خCO،¯µؤ³¤خھ_____£®
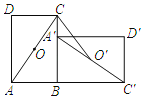
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬µبرü،÷ABCضذ£¬AB=AC£¬،دACB=72،م£¬

£¨1£©بôBD،حACسعD£¬اَ،دABDµؤ¶بت£»
£¨2£©بôCEئ½·ض،دACB£¬اَض¤£؛AE=BC£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
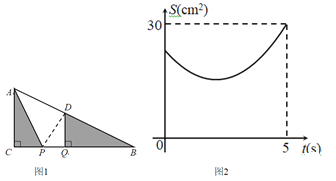
،¾جâؤ؟،؟بçح¼1£¬شعRt،÷ABCضذ£¬،دACB£½90،م£¬AC£½6cm.µمP،¢QتاBC±كةدء½¸ِ¶¯µم(µمQشعµمPسز±ك)£¬PQ£½2cm£¬µمP´سµمC³ِ·¢£¬رطCBدٍسزشث¶¯£¬شث¶¯ت±¼نخھtأë.5s؛َµمQµ½´ïµمB£¬µمP،¢Qح£ض¹شث¶¯£¬¹µمQ×÷QD،حBC½»ABسعµمD£¬ء¬½سAP£¬ةè،÷ACPسë،÷BQDµؤأو»؛حخھS(cm)£¬Sسëtµؤ؛¯تح¼دٌبçح¼2ثùت¾.
(1)ح¼1ضذBC£½ cm£¬µمPشث¶¯µؤثظ¶بخھ cm/s£»
(2)tخھ؛خضµت±£¬أو»؛حS×îذ،£¬²¢اَ³ِ×îذ،ضµ£»
(3)ء¬½سPD£¬زشµمPخھش²ذؤدك¶خPDµؤ³¤خھ°ë¾¶×÷،رP£¬µ±،رPسë![]() µؤ±كدàاذت±£¬اَtµؤضµ.
µؤ±كدàاذت±£¬اَtµؤضµ.
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com