
【题目】如图,已知在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是四个内角的平分线,
分别是四个内角的平分线,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() 求证:四边形
求证:四边形![]() 是正方形.
是正方形.

【答案】见解析.
【解析】
根据矩形的性质和角平分线定义易得△FDC、△MDA、△EAB、△NBC都是等腰直角三角形,则∠E=∠F=∠EMF=∠ENF=90°,可得四边形EMFN是矩形,然后证明△FDC≌△EAB,求出ME=MF即可证得结论.
证明:∵在矩形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是四个内角的平分线,
分别是四个内角的平分线,
∴∠FDC=∠FCD=45°,
∴△FDC是等腰直角三角形,
同理可得:△MDA、△EAB、△NBC都是等腰直角三角形,
∴∠E=∠F=∠EMF=∠ENF=90°,
∴四边形EMFN是矩形,
在△FDC和△EAB中,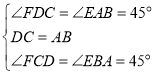 ,
,
∴△FDC≌△EAB(ASA),
∴FD=EA,
又∵MD=MA,
∴ME=MF,
∴矩形EMFN是正方形.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B,与反比例函数![]() (k>0)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若
(k>0)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若![]() ,则△OEF与△CEF的面积之比是( )
,则△OEF与△CEF的面积之比是( )
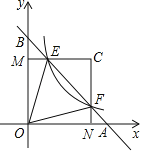
A.2:1B.3:1C.2:3D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“作已知角的角平分线”的尺规作图过程.
已知:如图,∠AOB.
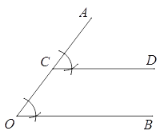
求作:∠AOB的角平分线OP.
作法:如图,
①在射线OA上任取点C;
②作∠ACD=∠AOB;
③以点C为圆心CO长为半径画圆,交射线CD于点P;
④作射线OP;
所以射线OP即为所求.
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:∵ ∠ACD=∠AOB,
∴ CD∥OB(____________)(填推理的依据).
∴∠BOP=∠CPO.
又∵ OC=CP,
∴∠COP=∠CPO(____________)(填推理的依据).
∴∠COP=∠BOP.
∴ OP平分∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界上最长的跨海大桥.如图是港珠澳大桥的海豚塔部分效果图,为了测得海豚塔斜拉索顶端A距离海平面的高度,先测出斜拉索底端C到桥塔的距离(CD的长)约为100米,又在C点测得A点的仰角为30°,测得B点的俯角为20°,求斜拉索顶端A点到海平面B点的距离(AB的长).(已知![]() ≈1.732,tan20°≈0.36,结果精确到0.1)
≈1.732,tan20°≈0.36,结果精确到0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙O的半径为1,点A在x轴的正半轴上,B为⊙O上一点,过点A、B的直线与y轴交于点C,且OA2=ABAC.

(1)求证:直线AB是⊙O的切线;
(2)若AB=![]() ,求直线AB对应的函数表达式.
,求直线AB对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com