
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为线段
为线段![]() 上两动点,且
上两动点,且![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.
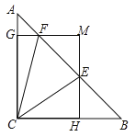
(1)求证:![]() ;
;
(2)试探究![]() 、
、![]() 、
、![]() 之间有何数量关系?说明理由.
之间有何数量关系?说明理由.
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,O为坐标原点,
中,O为坐标原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() 垂直于
垂直于![]() 轴,
轴,![]() ,
,![]() .若动点
.若动点![]() 、
、![]() 同时从点0出发,
同时从点0出发,![]() 点沿折线
点沿折线![]() 运动,到达
运动,到达![]() 点时停止;
点时停止;![]() 点沿
点沿![]() 运动,到达
运动,到达![]() 点时停止,它们运动的速度都是每秒1个单位长度。设
点时停止,它们运动的速度都是每秒1个单位长度。设![]() 运动
运动![]() 秒时,
秒时,![]() 的面积为
的面积为![]() (平方单位),则
(平方单位),则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
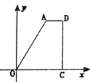
A.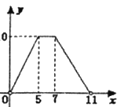 B.
B.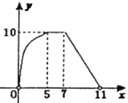
C.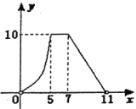
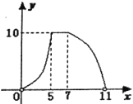
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=![]() .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
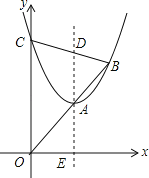
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
(1)转动转盘两次,用画树状图或列表的方法求两次指针所指区域数字不同的概率;
(2)在第(1)题中,两次转到的区域的数字作为两条线段的长度,如果第三条线段的长度为5,求这三条线段能构成三角形的概率.
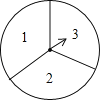
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列10×10的网格中,横、纵坐标均为整数的点叫做格点,例如A(3,0),B(4,3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD(点A,B的对应点分别为点C,D).
(1)作出△COD;
(2)下面仅用无刻度的直尺画△AOD的内心I,操作如下:
第一步:在x轴上找一格点E,连接DE,使OE=OD;
第二步:在DE上找一点F,连接OF,使OF平分∠AOD;
第三步:找格点G,得到正方形OAGC,连接AC,则AC与OF的交点I是△OAD的内心.
请你按步骤完成作图,并直接写出E,F,I三点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com