
����Ŀ������ABC�У�AB��12��AC��BC��10������ABC�Ƶ�A��˳ʱ�뷽����ת���õ���ADE����ת��Ϊ��(0��<��<180��)����B�Ķ�Ӧ��ΪD����C�Ķ�Ӧ��ΪE������BD��BE��
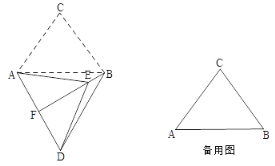
��1����ͼ��������60��ʱ���ӳ�BE��AD�ڵ�F��
����֤����ABD�ǵȱ������Σ�
����֤��BF��AD��AF��DF��
����ֱ��д��BE�ij���
��2������ת�����У�����D��DG��ֱ��ֱ��AB������ΪG������CE������DAG����ACB�����߶�DG���߶�AE������ʱ����ֱ��д��BE��CE��ֵ��
���𰸡���1����֤������������֤������������ BE��6![]() ��8����2��BE��CE��26 ��
��8����2��BE��CE��26 ��
��������
��1��������ת����֪AB=AD����BAD=60�����ɵ�֤��
����BA=BD��EA=ED�����߶δ�ֱƽ���ߵ����ʼ��ɵ�֤��
�۷ֱ����BF��EF�ij����ɵã�
��2���ɡ�ACB+��BAC+��ABC=180������DAG+��DAE+��BAE=180������DAG=��ACB����DAE=��BAC�á�BAE=��BAC��AE=AC���������ߺ�һ�ɵ�CE��AB��AC=10��AH=6���̶�֪CE=2CH=16��BE=10�����ɵô𰸣�
��1���١ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60���õ���ADE��
��AB=AD����BAD=60����
���ABD�ǵȱ������Σ�
���ɢٵá�ABD�ǵȱ������Σ�
��AB=BD��
�ߡ�ABC�Ƶ�A˳ʱ�뷽����ת60���õ���ADE��
��AC=AE��BC=DE��
�֡�AC=BC��
��EA=ED��
���B��E��AD���߶δ�ֱƽ�����ϣ�
��BE��AD���߶δ�ֱƽ���ߣ�
�ߵ�F��BE���ӳ����ϣ�
��BF��AD��AF=DF��
���ɢ�֪BF��AD��AF=DF��
��AF=DF=6��
��AE=AC=10��
��EF=8��
���ڵȱ�������ABD�У�BF=![]() ��
��
��BE=BF��EF=![]() ��
��
��2����ͼ��ʾ��
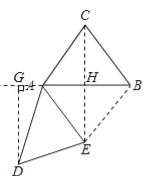
�ߡ�DAG=��ACB����DAE=��BAC��
���ACB+��BAC+��ABC=��DAG+��DAE+��ABC=180����
�֡ߡ�DAG+��DAE+��BAE=180����
���BAE=��ABC��
��AC=BC=AE��
���BAC=��ABC��
���BAE=��BAC��
��AB��CE����CH=HE=![]() CE��
CE��
��AC=BC��
��AH=BH=![]() AB=6��
AB=6��
��CH=![]()
��CE=2CH=16��BE=10��
��BE+CE=10+16=26��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪӭ�������п����˽�ѧ�������������ѧУ��������˱�У���꼶50��ѧ����30���������Ĵ����������������õ������������£�

��������ͼ����Ϣ������������⣺
��1�����е�a=����������c=����������
��2�����Ƶ���ֲ�ֱ��ͼ����������(��ͼ�����ע��Ӧ������)
��3������У���꼶����500��ѧ����������ơ�30���������Ĵ���60������(��60��)��ѧ���ж�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ɽɽ��������A���붫��B�����800(1��![]() )�ף�С����С��ͬʱ�ֱ��A����B����ɽ��C�������ߣ���֪ɽ�����˵��½���45�������˵��½���30����С���������ٶ�Ϊ
)�ף�С����С��ͬʱ�ֱ��A����B����ɽ��C�������ߣ���֪ɽ�����˵��½���45�������˵��½���30����С���������ٶ�Ϊ![]() ��/�룮��С����С��ͬʱ����ɽ��C������С���������ٶ��Ƕ��٣�
��/�룮��С����С��ͬʱ����ɽ��C������С���������ٶ��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��,��A,B������ֱ�Ϊ(1,0),(3,0)����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD.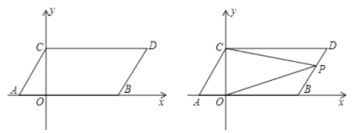
(1)���C,D�����꼰�ı���ABDC�����S�ı���ABDC��
(2)��y�����Ƿ����һ��P,����PA,PB,ʹS��PAB=S�ı���ABDC?����������һ�㣬�����P�����ꣻ�������ڣ���˵�����ɣ�
(3)��P��ֱ��BD��һ�����㣬����PC��PO������P��ֱ��BD���˶�ʱ����ֱ��д����OPC���PCD����POB��������ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ����ͼ����Ҫ��д��������Ҫ������ͼ�ۼ���
��1����ͼ1���ı���ABCD��ƽ���ı��Σ�EΪBC������һ�㣬��ֻ��ֱ���������̶ȣ��ڱ�AD���ҵ�F��ʹDF=BE��

��2����ͼ2��BE������ABCD�ı�AD�ϵĸߣ���ֻ��ֱ���������̶ȣ���������ABCD�ı�AB�ϵĸ�DF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����CΪ�߶�AB������һ�㣨�����A��B�غϣ����ֱ���AC��BCΪһ����AB��ͬ����������ACD�͡�BCE��CA��CD��CB��CE����ACD����BCE��30�㣬����AE��CD�ڵ�M������BD��CE�ڵ�N��AE��BD���ڵ�P������CP��
��1���߶�AE��DB��������ϵΪ�� ����ֱ��д����APD���� ��
��2������BCE�Ƶ�C��ת����ͼ2��ʾ��λ�ã������������䣬̽���߶�AE��DB��������ϵ����˵�����ɣ������ʱ��APD�Ķ�����
��3���ڣ�2������������֤����APC����BPC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�У�![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ������Ϊ
������Ϊ![]() ��
��
��1��![]() ��
��![]() ƽ����Ϊʲô��
ƽ����Ϊʲô��
��2�����![]() ����
����![]() ����
����![]() �Ķ���.
�Ķ���.
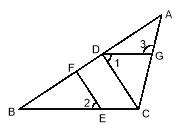
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬����
Ϊ����ԭ�㣬����![]() �ĶԽ���
�ĶԽ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ����ֱ��ڵ�һ���͵�������.ֱ��
����ֱ��ڵ�һ���͵�������.ֱ��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��

��1����ͼ1�����![]() �����ꣻ
�����ꣻ
��2����ͼ2��![]() Ϊ����
Ϊ����![]() ��һ���㣨�����
��һ���㣨�����![]() �͵�
�͵�![]() �غϣ�������
�غϣ�������![]() ��
��![]() �ύֱ��
�ύֱ��![]() �ڵ�
�ڵ�![]() .���߶�
.���߶�![]() �ij���Ϊ
�ij���Ϊ![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ����ֱ��д���Ա���
�ĺ�����ϵʽ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����ͼ3���ڣ�2���������£�����![]() �˶����߶�
�˶����߶�![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ���Ľ�ƽ����
���Ľ�ƽ����![]() ��
��![]() ���ڵ�
���ڵ�![]() �����
�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��![]() �����ۣ���
�����ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�����У� ��
��������ȷ�����У� ��

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com