
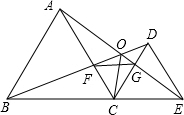
 如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④OE=OD+OC.其中正确结论的个数 ( )
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④OE=OD+OC.其中正确结论的个数 ( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由等边三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,证出∠ACE=∠BCD,由SAS证明△AC≌△BCE,得出AE=BD,①正确;∠CAG=∠CBF,由AAS证明△ACG≌△BCF,得出AG=BF,CG=CF,②正确;证明△CFG是等边三角形,得出∠GFC=∠ACB,证出FG∥BE;③正确;在OE上截取OG=OD,连接DM,由SAS证明△DME≌△DOC,得出ME=OC,得出④正确;即可得出结论.
解答 解:∵△ABC和△CDE均是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACE=∠BCD}&{\;}\\{CE=CD}&{\;}\end{array}\right.$,
∴△AC≌△BCE(SAS),
∴AE=BD,①正确;
∠CAG=∠CBF,
∵∠ACG=180°-2×60°=60°,
∴∠ACG=∠BCF=60°,
在△ACG和△BCF中,
$\left\{\begin{array}{l}{∠ACG=∠BCF}&{\;}\\{∠CAG=∠CBF}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△ACG≌△BCF(AAS),
∴AG=BF,CG=CF,②正确;
∵∠ACG=60°,
∴△CFG是等边三角形,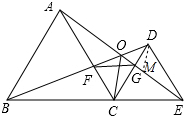
∴∠GFC=60°=∠ACB,
∴FG∥BE;③正确;
在OE上截取OM=OD,连接DM,如图所示:
∵∠DOM=∠OBC+∠OEB=∠CAG+∠OEB=60°,
∴△ODM是等边三角形,
∴OD=DM,∠ODG=∠CDE=60°,
∴∠ODC=∠MDE,
在△DME和△DOC中,
$\left\{\begin{array}{l}{DM=OD}&{\;}\\{∠MDE=∠ODC}&{\;}\\{DE=DC}&{\;}\end{array}\right.$,
∴△DME≌△DOC(SAS),
∴ME=OC,
∵OE=OM+ME,
∴OE=OD+OC,④正确;
故选D.
点评 本题考查了全等三角形的判定和性质,等边三角形的判定与性质,平行线的判定等知识;熟练掌握等边三角形的性质,证明三角形全等是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
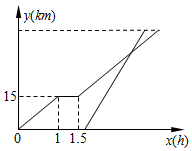 周末,小华骑自行车从家出发到植物园玩,从家出发1小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华从家出发1小时50分后,爸爸从家出发骑摩托车沿相同路线前往植物园,如图是他们家的路程y(km)与小华离家的时间x(h)的函数图象,已知爸爸骑摩托车的速度是小华骑车速度的2倍,若爸爸比小华早10分达到植物园,则小华家到植物园的路程是45km.
周末,小华骑自行车从家出发到植物园玩,从家出发1小时后,因自行车损坏修理了一段时间后,按原速前往植物园,小华从家出发1小时50分后,爸爸从家出发骑摩托车沿相同路线前往植物园,如图是他们家的路程y(km)与小华离家的时间x(h)的函数图象,已知爸爸骑摩托车的速度是小华骑车速度的2倍,若爸爸比小华早10分达到植物园,则小华家到植物园的路程是45km.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 买一张电影票,座位号是奇数 | |
| B. | 从一个只装有红球的袋子里摸出白球 | |
| C. | 三角形两边之和大于第三边 | |
| D. | 明天会下雨 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
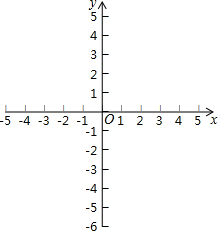 已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).
已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com