
 在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.
在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD在第一象限,四边分别平行于x轴和y轴,且顶点A、C在反比例函数图象上,BA延长线交y轴于点E,BC延长线交x轴于点F,S△AOE=$\frac{1}{2}$.
如图,矩形ABCD在第一象限,四边分别平行于x轴和y轴,且顶点A、C在反比例函数图象上,BA延长线交y轴于点E,BC延长线交x轴于点F,S△AOE=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 王华期末考试数学成绩会是100分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
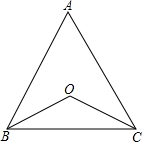 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 成绩(分) | 46 | 47 | 48 | 49 | 50 |
| 人数(人) | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名同学的体育成绩的众数为50 | |
| B. | 这10名同学的体育成绩的中位数为48 | |
| C. | 这10名同学的体育成绩的方差为50 | |
| D. | 这10名同学的体育成绩的平均数为48 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
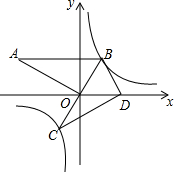 在平面直角坐标系中双曲线$y=\frac{k}{x}$经过△CDB顶点B,边BC过坐标原点O,点D在x轴的正半轴上,且∠BDC=90°,现将△CDB绕点B顺时针旋转得到对应△AOB如图所示,此时AB∥x轴,OA=$2\sqrt{3}$.则k的值是( )
在平面直角坐标系中双曲线$y=\frac{k}{x}$经过△CDB顶点B,边BC过坐标原点O,点D在x轴的正半轴上,且∠BDC=90°,现将△CDB绕点B顺时针旋转得到对应△AOB如图所示,此时AB∥x轴,OA=$2\sqrt{3}$.则k的值是( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com