
【题目】如图,在平面直角坐标系中,点A(2,3),抛物线G:y=x2-2x+c(c为常数)的顶点坐标为M,其对称轴与x轴相交于点N.
(1)若抛物线G经过点A,求出其解析式,并写出点M的坐标.
(2)若点B(x1,y1)和点C(x1+3,y2)在抛物线G上,试比较y1,y2的大小.
(3)连接OM,若45°≤∠MON≤60°,请直接写出c的取值范围.
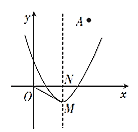
【答案】(1)(1,2)(2)当x>-![]() 时,y2>y1;当x=-
时,y2>y1;当x=-![]() 时,y2=y1;当x<-
时,y2=y1;当x<-![]() 时,y2<y1;(3)2≤c≤1+
时,y2<y1;(3)2≤c≤1+![]() 或1-
或1-![]() ≤c≤0
≤c≤0
【解析】
(1)把点A代入抛物线解析式求出c的值 ,得到抛物线的解析式进行配方即可得到M的坐标;
(2)先确定抛物线的对称轴,再将点B与点C分三种位置关系讨论求解即可;
(3)分别求出∠MON=45°时和∠MON=60°时c的值,即可求出45°≤∠MON≤60°时,c的取值范围.
把A(2,3)代入抛物线得4-4+c=3,
解得c=3,
∴y=x2-2x+3=(x-1)2+2
∴M(1,2);
(2)∵y=x2-2x+c,
∴对称轴为:x=1,
∴当x≤1时,y随x的增大而减小,当x≥1时,y随x的增大而增大,
①当B、C都在对称轴左侧时,x1+3≤1即x1≤-2时,y1>y2;
②当B、C都在对称轴右侧时,x1≥1时,y1<y2;
③当B在对称轴左侧、C在对称轴右侧时,x1<1且x1+3>1,
∴-2<x1<1
点B关于x=1的对称点为(2-x1,y1)
当2-x1<x1+3时,x1>-![]() ,y1<y2,
,y1<y2,
当2-x1>x1+3时,x1<-![]() ,y1>y2,
,y1>y2,
当2-x1=x1+3时,x1=-![]() ,y1=y2,
,y1=y2,
综上所述,
当x>-![]() 时,y2>y1;当x=-
时,y2>y1;当x=-![]() 时,y2=y1;当x<-
时,y2=y1;当x<-![]() 时,y2<y1;
时,y2<y1;
(3)∵y=x2-2x+c=(x-1)2+c-1,
∴顶点坐标为M(1,c-1),
∵对称轴与x轴交于点N,
∴N(1,0)
∴ON=1,
当∠MON=45°时,在Rt△MON中,![]() ,
,
∴|c-1|=1,
∴c=2或c=0;
当∠MON=60°时,在Rt△MON中,![]() ,
,
∴|c-1|=![]() ,
,
∴c=![]() +1或c=1-
+1或c=1-![]() ,
,
∴当45°≤∠MON≤60°时,2≤c≤1+![]() 或1-
或1-![]() ≤c≤0.
≤c≤0.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+3的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△APC的面积为5,求点P的坐标;
(3)直接写出不等式﹣x+3<![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中有这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?其大意如下:今有5只雀、6只燕,分别放一起用衡器称,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置放,两边重量相等.5只雀、6只燕重量为1斤(注:声代1斤=16两).问每只雀、燕各重多少两?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数).
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点;
(2)设抛物线的顶点为A,与x轴两个交点分别为B,D,B在D的右侧,与y轴的交点为C.
①求证:当m取不同值时,△ABD都是等边三角形;
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点D,E分别在BC,AC上,且DC=AE,AD与BE交于点P,连接PC.
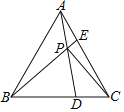
(1)证明:ΔABE≌ΔCAD.
(2)若CE=CP,求证∠CPD=∠PBD.
(3)在(2)的条件下,证明:点D是BC的黄金分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
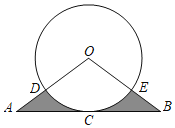
【题目】如图,AB与⊙O相切于点C,OA、OB分别交⊙O于点D、E、弧CD=弧CE
(1)求证:∠A=∠B.
(2)已知AC=2![]() ,OA=4,求阴影部分的面积.(结果保留根号和π)
,OA=4,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com