
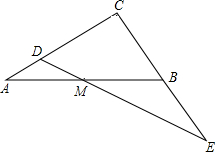
 如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.
如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.分析 (1)过B作BF∥AC交DE于F,通过△ADM≌△BFM,得到AD=BF=x,由于△EBF∽△ECD,得到$\frac{BF}{CD}=\frac{BE}{CE}$,于是得到$\frac{x}{1-x}=\frac{y}{1+y}$,即可得到结论;
(2)以AD、BE为两边不能构成一个等腰直角三角形,以AD,BE分别为斜边时,把y=$\frac{\sqrt{2}}{2}$x或y=$\sqrt{2}$x,分别代入(1)中的解析式得到x值,由(1)知:0<x<$\frac{1}{2}$,于是得到以AD、BE为两边不能构成一个等腰直角三角形.
解答 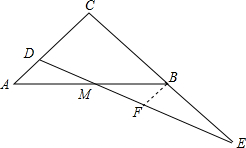 解:过B作BF∥AC交DE于F,
解:过B作BF∥AC交DE于F,
∴∠A=∠ABF,
∵M为边AB中点,
∴AM=BM,
在△ADM与△BFM中,
$\left\{\begin{array}{l}{∠A=∠MBF}\\{AM=BM}\\{∠AMD=∠BMF}\end{array}\right.$,
∴△ADM≌△BFM,
∴AD=BF=x,
∵AC=BC=1,
∴CD=1-x,CE=1+y,
∵BF∥AC,
∴△EBF∽△ECD,
∴$\frac{BF}{CD}=\frac{BE}{CE}$,
即:$\frac{x}{1-x}=\frac{y}{1+y}$,
∴y=$\frac{x}{1-2x}$ (0<x<$\frac{1}{2}$);
(2)以AD、BE为两边不能构成一个等腰直角三角形,
理由:当以AD为斜边,则y=$\frac{\sqrt{2}}{2}$x,
∴$\frac{\sqrt{2}}{2}$x=$\frac{x}{1-2x}$,
解得:x=$\frac{\sqrt{2}-2}{2\sqrt{2}}$<0,
当以BE为斜边,则y=$\sqrt{2}$x,
∴$\sqrt{2}$x=$\frac{x}{1-2x}$,
解得:x=$\frac{1}{2}$,
由(1)知:0<x<$\frac{1}{2}$,
∴以AD、BE为两边不能构成一个等腰直角三角形.
点评 本题考查了等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,求函数的解析式,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
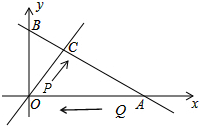 如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
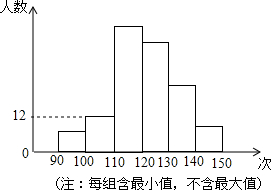 九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题
九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,测试成绩整理后作出如图统计图,甲同学计算出前两组的频率和是0.12,乙同学计算出第一组的频率和为0.04,丙同学计算出从左至右第二、三、四组的频数比为4:17:15,结合统计图回答下列问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com