
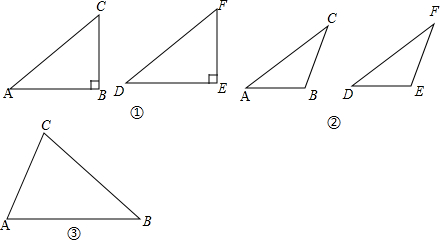
���� ��1��ֱ������HL�����ó�Rt��ABC��Rt��DEF��
��2�����ȵó���CBG�ա�FEH��AAS������CG=FH�������ó�Rt��ACG��Rt��DFH���������ABC�ա�DEF��
��3��������֪ͼ������һ���۽������μ��ɵó��𰸣�
��4�����ã�3���з����ɵó�����B�ݡ�Aʱ�����ABC�ա�DEF��
��� ��1���⣺��ͼ�٣�
�ߡ�B=��E=90�㣬
����Rt��ABC��Rt��DEF��
$\left\{\begin{array}{l}{AC=DF}\\{BC=EF}\end{array}\right.$��
��Rt��ABC��Rt��DEF��HL����
�ʴ�Ϊ��HL��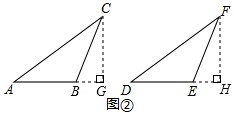 ��2��֤������ͼ�ڣ�����C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H��
��2��֤������ͼ�ڣ�����C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H��
�ߡ�ABC=��DEF���ҡ�ABC����DEF���Ƕ۽ǣ�
��180��-��ABC=180��-��DEF��
����CBG=��FEH��
�ڡ�CBG�͡�FEH�У�
$\left\{\begin{array}{l}{��CBG=��FEH}\\{��G=��H=90��}\\{BC=EF}\end{array}\right.$��
���CBG�ա�FEH��AAS����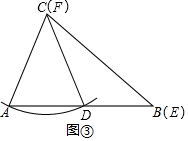
��CG=FH��
��Rt��ACG��Rt��DFH��
$\left\{\begin{array}{l}{AC=DF}\\{CG=FH}\end{array}\right.$��
��Rt��ACG��Rt��DFH��HL����
���A=��D��
�ڡ�ABC�͡�DEF�У�
$\left\{\begin{array}{l}{��A=��D}\\{��ABC=��DEF}\\{AC=DF}\end{array}\right.$��
���ABC�ա�DEF��AAS����
��3���⣺��ͼ���У��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E��
��DEF�͡�ABC��ȫ�ȣ�
��4���⣺��ͼ�ۿ�֪����A=��CDA=��B+��BCD��
���A����B��
�൱��B�ݡ�Aʱ����ABC��Ψһȷ���ˣ�
���ABC�ա�DEF��
�ʴ�Ϊ����B�ݡ�A��
���� ���⿼����ȫ�������ε��ж������ʣ�Ӧ���������ͼ����������������ȫ�ȵ��ж������ǽ���Ĺؼ����Ķ����ϴ�����Ҫ������ϸ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
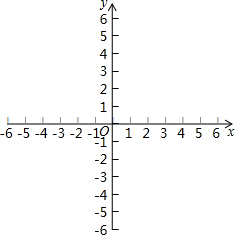 ��������y=2x+4��ͼ������ͼ��
��������y=2x+4��ͼ������ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com