
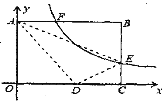
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
【答案】A
【解析】
首先根据翻折变换的性质,可得AD=AB=10,DE=BE;然后设点E的坐标是(10,b),在Rt△CDE中,根据勾股定理,求出CE的长度,进而求出k的值是多少;最后用k的值除以点F的纵坐标,求出线段AF的长为多少即可.
∵△ABE沿AE折叠,点B刚好与OC边上点D重合,
∴AD=AB=10,DE=BE,
∵AO=8,AD=10,
∴OD=![]() =6,CD=10-6=4,
=6,CD=10-6=4,
设点E的坐标是(10,b),
则CE=b,DE=10-b,
∵CD2+CE2=DE2,
∴42+b2=(8-b)2,
解得b=3,
∴点E的坐标是(10,3),
∴k=10×3=30,
∴线段AF的长为:
30÷8=![]() .
.
故选:A.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 、
、![]() 在坐标轴上,点
在坐标轴上,点![]() 坐标
坐标![]() ,将正方形
,将正方形![]() 绕点
绕点![]() 顺时针旋转角度
顺时针旋转角度![]() ,得到正方形
,得到正方形![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,
,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,连
,连![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数,并判断线段
的度数,并判断线段![]() 、
、![]() 、
、![]() 之间的数量关系,说明理由;
之间的数量关系,说明理由;
(3)当![]() 时,求直线
时,求直线![]() 的解析式.
的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.

(1)探究:线段BM,MN,NC之间的关系,并加以证明。
(2)若点M是AB的延长线上的一点,N是CA的延长线上的点,其它条件不变,请你再探线段BM,MN,NC之间的关系,在图②中画出图形,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米,则路灯的高为 米.

查看答案和解析>>
科目:初中数学 来源: 题型:
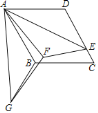
【题目】如图,在菱形ABCD中,![]() ,点E在边CD上,且
,点E在边CD上,且![]() ,
,![]() 与
与![]() 关于AE所在的直线成对称图形
关于AE所在的直线成对称图形![]() 以点A为中心,把
以点A为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接GF,则线段GF的长为______.
,连接GF,则线段GF的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com