
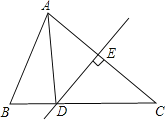
【题目】已知:在△ABC中,DE是AC的垂直平分线,AE=3.
①若AC=BC,求BC;
②若△ABD的周长为13,求△ABC的周长.
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】王大伯计划在自家的鱼塘里投放普通鱼苗和红色鱼苗,需要购买这两种鱼苗2000尾,购买这两种鱼苗的相关信息如下表:
品种项目 | 单价(元/尾) | 养殖费用(元/尾) |
普通鱼苗 | 0.5 | 1 |
红色鱼苗 | 1 | 1 |
设购买普通鱼苗x尾,养殖这些鱼苗的总费用为y元.
(1)写出y(元)与x(尾)之间的函数关系式;
(2)如果购买每种鱼苗不少于600尾,在总鱼苗2000尾不变的条件下,养殖这些鱼苗的最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:
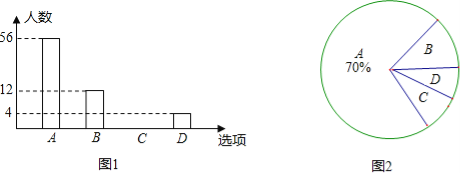
(1)本次调查共选取 名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
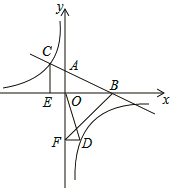
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为![]() 元,则可卖出(350-10
元,则可卖出(350-10![]() )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(1)班的学习小组学习“线段中点”内容时,得到一个很有意思的结论,请跟随他们一起思考.
(1)发现:
如图1,线段![]() ,点
,点![]() 在线段
在线段![]() 上,当点
上,当点![]() 是线段
是线段![]() 和线段
和线段![]() 的中点时,线段
的中点时,线段![]() 的长为_________;若点
的长为_________;若点![]() 在线段
在线段![]() 的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段
的延长线上,其他条件不变(请在图2中按题目要求将图补充完整),得到的线段![]() 与线段
与线段![]() 之间的数量关系为_________.
之间的数量关系为_________.
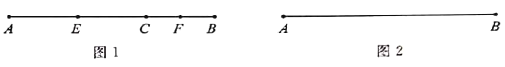
(2)应用:
如图3,现有长为40米的拔河比赛专用绳![]() ,其左右两端各有一段(
,其左右两端各有一段(![]() 和
和![]() )磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳
)磨损了,磨损后的麻绳不再符合比赛要求. 已知磨损的麻绳总长度不足20米. 小明认为只利用麻绳![]() 和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳
和一把剪刀(剪刀只用于剪断麻绳)就可以得到一条长20米的拔河比赛专用绳![]() . 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳
. 小明所在学习小组认为此法可行,于是他们应用“线段中点”的结论很快做出了符合要求的专用绳![]() ,请你尝试着“复原”他们的做法:
,请你尝试着“复原”他们的做法:
①在图中标出点![]() 、点
、点![]() 的位置,并简述画图方法;
的位置,并简述画图方法;
②请说明①题中所标示![]() 点的理由.
点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,已知在纸面上有一数轴(如图),折叠纸面.
![]()
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与何数表示的点重合;
(2)若﹣1表示的点与5表示的点重合,0表示的点与何数表示的点重合;
(3)若﹣1表示的点与5表示的点之间的线段折叠2次,展开后,请写出所有的折点表示的数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
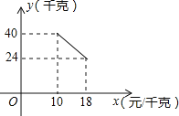
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?
(3)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com