
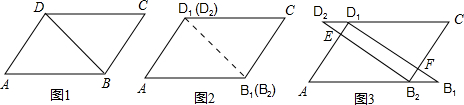
 =
= ,B2B1=x
,B2B1=x x
x x
x x•(8-
x•(8- x)
x)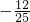 (x-5)2+12(0<x<10)
(x-5)2+12(0<x<10)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
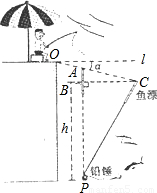
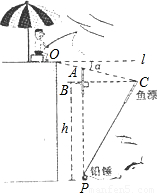
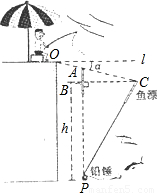
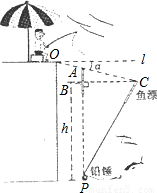
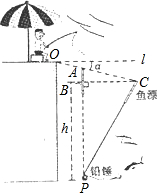 如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来,假设铅垂P不动,鱼漂移动了一段距离BC,且顶端恰好与水面齐平,(即PA=PC)水平l与OC的夹角α为8°(点A在OC上),求铅锤P处的水深h.
如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来,假设铅垂P不动,鱼漂移动了一段距离BC,且顶端恰好与水面齐平,(即PA=PC)水平l与OC的夹角α为8°(点A在OC上),求铅锤P处的水深h.查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(35):7.6 锐角三角函数的简单应用(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第28章《锐角三角函数》中考题集(34):28.2 解直角三角形(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2013年4月中考数学模拟试卷(45)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年安徽省安庆市岳西县姚河中学中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com