
 (2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
(2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
|
|
| 2 |
| 3 |


科目:初中数学 来源: 题型:
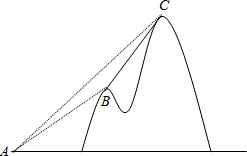 (2012•瑶海区三模)如图,某电信公司计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长.(结果可保留根号)
(2012•瑶海区三模)如图,某电信公司计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长.(结果可保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
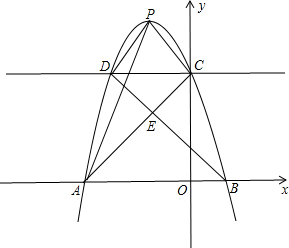 (2012•瑶海区三模)已知抛物线y=ax2+bx+c(a≠0)过点A(-3,0),B(1,0),C(0,3)三点.
(2012•瑶海区三模)已知抛物线y=ax2+bx+c(a≠0)过点A(-3,0),B(1,0),C(0,3)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com