
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
【答案】(1)证明见解析(2)y=![]() x+2(0<x<2
x+2(0<x<2![]() )(3)当△ADE是等腰三角形时,AE=4﹣2
)(3)当△ADE是等腰三角形时,AE=4﹣2![]() 或
或![]() .
.
【解析】
试题分析:(1)根据两角相等证明:△ABD∽△DCE;
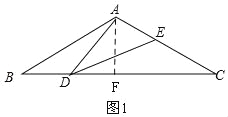
(2)如图1,作高AF,根据直角三角形30°的性质求AF的长,根据勾股定理求BF的长,则可得BC的长,根据(1)中的相似列比例式可得函数关系式,并确定取值;
(3)分三种情况进行讨论:①当AD=DE时;②当AE=ED时;③当AD=AE时,讨论即可得到答案.
试题解析:(1)∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°,
∴∠ABD=∠ADE=30°,
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE;
(2)如图1,∵AB=AC=2,∠BAC=120°,
过A作AF⊥BC于F,
∴∠AFB=90°,
∵AB=2,∠ABF=30°,
∴AF=![]() AB=1,
AB=1,
∴BF=![]() ,
,
∴BC=2BF=2![]() ,
,
则DC=2![]() ﹣x,EC=2﹣y,
﹣x,EC=2﹣y,
∵△ABD∽△DCE,
∴![]() ,
,
∴![]() ,
,
化简得:y=![]() x+2(0<x<2
x+2(0<x<2![]() );
);
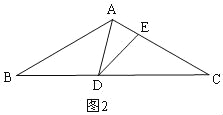
(3)当AD=DE时,如图2,
由(1)可知:此时△ABD∽△DCE,
则AB=CD,即2=2![]() ﹣x,
﹣x,
x=2![]() ﹣2,代入y=
﹣2,代入y=![]() x+2,
x+2,
解得:y=4﹣2![]() ,即AE=4﹣2
,即AE=4﹣2![]() ,
,
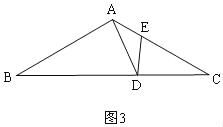
当AE=ED时,如图3,
∠EAD=∠EDA=30°,∠AED=120°,
∴∠DEC=60°,∠EDC=90°,
则ED=![]() EC,即y=
EC,即y=![]() (2﹣y),
(2﹣y),
解得:y=![]() ,即AE=
,即AE=![]() ,
,
当AD=AE时,
∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在,
∴当△ADE是等腰三角形时,AE=4﹣2![]() 或
或![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图(1),等边△ABC 中,D 是 AB 边上的动点,以 CD 为一边,向上作等边△EDC,连接AE.
(1)△DBC 和△EAC 会全等吗?请说说你的理由;
(2)试说明 AE∥BC 的理由;
(3)如图(2),将(1)动点 D 运动到边 BA 的延长线上,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
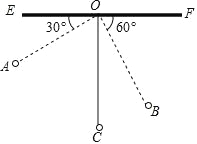
【题目】如图,物理老师为同学们演示单摆运动,单摆左右摆动中,在![]() 的位置时俯角
的位置时俯角![]() ,在
,在![]() 的位置时俯角
的位置时俯角![]() .若
.若![]() ,点
,点![]() 比点
比点![]() 高
高![]() .
.
求(1)单摆的长度(![]() );
);
(2)从点![]() 摆动到点
摆动到点![]() 经过的路径长(
经过的路径长(![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距300千米,甲、乙两辆汽车同时分别从A、B两地相向而行,假设它们都保持匀速行驶,则它们各自到A地的距离s(千米)都是行驶时间t(时)的一次函数,图象如图所示,请利用所结合图象回答下列问题: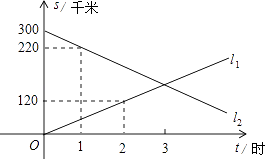
(1)甲的速度为 , 乙的速度为;
(2)求出:l1和l2的关系式;
(3)问经过多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
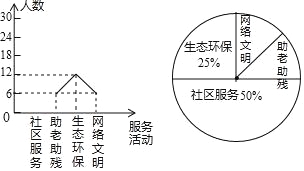
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:6cos45°+(![]() )﹣1+(
)﹣1+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017
|+42017×(﹣0.25)2017
(2)先化简,再求值:(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号 .
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com