
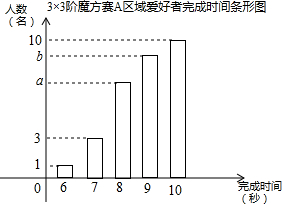
 某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:
某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:分析 ①由图知1人6秒,3人7秒,小于8秒的爱好者共有4人,进入下一轮角逐的人数比例为4:30;
②因为其他赛区情况大致一致,所以进入下一轮的人数为:600×A区进入下一轮角逐的人数比例;
③由完成时间的平均值和A区30人,得到关于a、b的二元一次方程组,求出a、b,得到完成时间8秒的爱好者的概率.
解答 解:①A区小于8秒的共有3+1=4(人)
所以A区进入下一轮角逐的人数比例为:$\frac{4}{30}$=$\frac{2}{15}$;
②估计进入下一轮角逐的人数为600×$\frac{2}{15}$=80(人);
③因为A区域爱好者完成时间的平均值为8.8秒,
所以(1×6+3×7+a×8+b×9+10×10)÷30=8.8
化简,得8a+9b=137
又∵1+3+a+b+10=30,即a+b=16
所以$\left\{\begin{array}{l}{8a+9b=137}\\{a+b=16}\end{array}\right.$
解得a=7,b=9
所以该区完成时间为8秒的爱好者的概率为$\frac{7}{30}$.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.解决本题的关键是根据平均数和各个时间段的人数确定完成时间为8秒的人数.概率=所求情况数与总情况数之比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
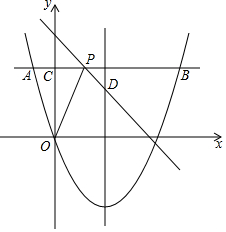 如图,过抛物线y=$\frac{1}{4}$x2-2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为-2.
如图,过抛物线y=$\frac{1}{4}$x2-2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
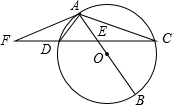 如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.
如图,已知AB是⊙O的直径,弦CD交AB于点E,作∠DAF=∠ACD,交CD延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com