
| A. | -a-2 | B. | -$\frac{1}{a+2}$ | C. | $\frac{1}{a+2}$ | D. | $\frac{1}{a-2}$ |
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
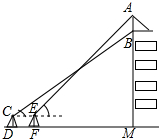 小华周末去汉唐书城买书,发现书城所在的大楼的楼顶有一面大约3m高的旗帜(如图所示),于是他想利用所学知识测量下书城所在大楼的高度,小华在楼前空地上的点D处,用1.3米高的测角仪CD从点C测得旗帜的底部B的仰角为35°,然后向教学楼正方向走了5米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.已知点A、B、M在同一直线上,CD⊥DM,EF⊥DM,请根据以上数据,求这座大楼的高度BM.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.结果精确到0.1m).
小华周末去汉唐书城买书,发现书城所在的大楼的楼顶有一面大约3m高的旗帜(如图所示),于是他想利用所学知识测量下书城所在大楼的高度,小华在楼前空地上的点D处,用1.3米高的测角仪CD从点C测得旗帜的底部B的仰角为35°,然后向教学楼正方向走了5米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.已知点A、B、M在同一直线上,CD⊥DM,EF⊥DM,请根据以上数据,求这座大楼的高度BM.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.结果精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
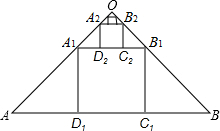 如图,等腰直角三角形OAB中,∠AOB=90°,AB=1,在△OAB中作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$.
如图,等腰直角三角形OAB中,∠AOB=90°,AB=1,在△OAB中作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,四边形ABCD中,DB⊥BC,DB平分∠ADC,点E为边CD的中点,AB⊥BE.
已知:如图,四边形ABCD中,DB⊥BC,DB平分∠ADC,点E为边CD的中点,AB⊥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com