
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() ;(3)
;(3)![]() 且
且![]() 且
且![]() .
.
【解析】
(1) 把![]() 代入
代入![]() 中可求出a的值;
中可求出a的值;
(2)讨论:当![]() , 即a> 1时,根据一次函数的性质得到x=3时,y=2,然后把(3,2)代入
, 即a> 1时,根据一次函数的性质得到x=3时,y=2,然后把(3,2)代入![]() 中求Ha得到此时一次函数解析式;当a-1<0, 即a<1时,利用一次函数的性质得到x=-2时,y=2,然后把(-2,2) 代入
中求Ha得到此时一次函数解析式;当a-1<0, 即a<1时,利用一次函数的性质得到x=-2时,y=2,然后把(-2,2) 代入![]() 中求出a得到此时一次函数解析式;
中求出a得到此时一次函数解析式;
(3)先整理得到![]() ,再对一切实数x,
,再对一切实数x,![]() 都成立,则直线y与y平行,且y在y的上方,所以
都成立,则直线y与y平行,且y在y的上方,所以![]() 且
且![]() ,从而得到a,m需满足的数量关系及a的取值范围.
,从而得到a,m需满足的数量关系及a的取值范围.
(1) 把![]() 代入
代入![]() 得
得![]() ,
,
![]() ;
;
(2)当a-1>0,即a> 1时,则x=3时,y=2,
把(3,2)代入![]() 得
得![]() ,解得a=4,此时一次函数解析式为
,解得a=4,此时一次函数解析式为![]() ;
;
当a-1<0,即a<1时,则x=-2时,y=2,
把(-2,2)代入![]() 得
得![]() ,解得
,解得![]() ,此时一.次函数解析式为
,此时一.次函数解析式为![]() ;
;
(3)![]() ,
,
∵对一切实数x,![]() 都成立,
都成立,
![]() 且
且![]() ,
,
![]() 且
且![]() 且
且![]()


科目:初中数学 来源: 题型:
【题目】如图,以直线![]() 上一点
上一点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将一个直角三角形的直角顶点放在点
,将一个直角三角形的直角顶点放在点![]() 处,(注,
处,(注,![]() )
)
(1)如图①,若直角三角板![]() 的一边
的一边![]() 放在射线
放在射线![]() 上,则
上,则![]() ______°;
______°;
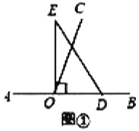
(2)如图②,将直角三角板![]() 绕点
绕点![]() 逆时针方向转动到某个位置,若
逆时针方向转动到某个位置,若![]() 恰好平分
恰好平分![]() ,求
,求![]() 的度数;
的度数;
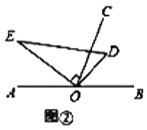
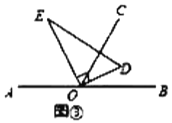
(3)如图③,将直角三角板![]() 绕点
绕点![]() 转动,如果
转动,如果![]() 始终在
始终在![]() 的内部,试猜想
的内部,试猜想![]() 和
和![]() 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
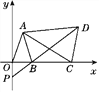
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且|a+b-3|+(a-2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)求证:AO=AB;
(2)求证:△AOC≌△ABD;
(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
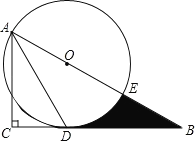
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学社团活动中,指导老师给同学们提出了以下问题:
问题:有67张卡片叠在一起,按从上而下的顺序先把第一张拿走,把第二张放到底层,然后把第三张拿走,再把第四张放到底层,如此进行下去,直至只剩最后一张卡片.问仅剩的这张卡片是原来的第几张卡片?
由于卡片数量较多,指导老师建议同学们先对较少的张数进行尝试,以便熟悉游戏规则并发现一些规律!
(1)请你试着在草稿纸上进行试验,将试验结果填写在下表中:
试验的卡片数量 (张) | 2 | 4 | 8 | 9 | 10 | 11 |
剩下最后一张卡片是 原来卡片的第几张 |
(2)根据试验结果的规律,回答最初的67张卡片情形,请你给出答案并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
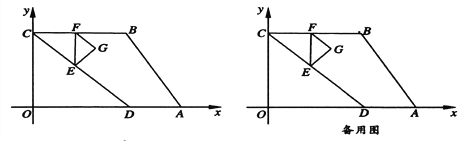
【题目】如图,四边形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半抽上,点
轴的正半抽上,点![]() 是
是![]() 上的一点,
上的一点,![]() ,点
,点![]() 的坐标为
的坐标为![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿线段
个单位长度的速度沿线段![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 的垂线
的垂线![]() 交线段
交线段![]() 于点
于点![]() ,以线段
,以线段![]() 为斜边向右作等腰直角
为斜边向右作等腰直角![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1) 点F的坐标为( , )点![]() 的坐标为( , )(用含
的坐标为( , )(用含![]() 的代数式表示),
的代数式表示),
(2)连接![]() 、
、![]() ,当
,当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)设点![]() 从点
从点![]() 出发时,点
出发时,点![]() 、
、![]() 、
、![]() 都与点
都与点![]() 重合,点
重合,点![]() 在运动过程中,当
在运动过程中,当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 运动的时间
运动的时间![]() 的值﹒
的值﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=150,∠AOC=40,OE是∠AOB内部的一条射线,OF平分∠AOE, 且OF在OC的右侧.
(1)若∠EOB=10,求∠COF的度数;
(2)若∠COF=20,求∠EOB的度数;
(3)若∠COF=n,求∠EOB的度数(用含n的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com