
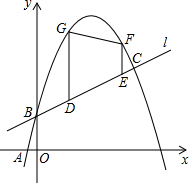
 如图,已知一次函数y1=$\frac{1}{2}$x+b的图象1与二次函数y2=-x2+mx+b的图象都经过点B(0,1)和点C,且二次函数的图象经过点A(2-$\sqrt{5}$,0)
如图,已知一次函数y1=$\frac{1}{2}$x+b的图象1与二次函数y2=-x2+mx+b的图象都经过点B(0,1)和点C,且二次函数的图象经过点A(2-$\sqrt{5}$,0)分析 (1)首先利用待定系数法求出二次函数解析式,然后求出其最大值;
(2)联立y1与y2,求出点C的坐标为C($\frac{7}{2}$,$\frac{11}{4}$),因此使y2>y1成立的x的取值范围为0<x<$\frac{7}{2}$,得s=1+2+3=6;
(3)四边形DEFG是一个梯形,将其面积用含有未知数的代数式表示出来,这个代数式是一个二次函数,根据其最值求出未知数的值,进而得到面积最大时点D、E的坐标.
解答 解:(1)∵二次函数y2=-x2+mx+b经过点B(0,1)与A(2-$\sqrt{5}$,0),
∴$\left\{\begin{array}{l}{b=1}\\{-(2-\sqrt{5})^{2}+(2-\sqrt{5})m+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{b=1}\end{array}\right.$
∴l:y1=$\frac{1}{2}$x+1;
∴y2=-x2+4x+1=-(x-2)2+5,
∴ymax=5;
(2)联立y1与y2得:$\frac{1}{2}$x+1=-x2+4x+1,解得x=0或x=$\frac{7}{2}$,
当x=$\frac{7}{2}$时,y1=$\frac{1}{2}$×$\frac{7}{2}$+1=$\frac{11}{4}$,
∴C($\frac{7}{2}$,$\frac{11}{4}$).
使y2>y1成立的x的取值范围为0<x<$\frac{7}{2}$,
∴s=1+2+3=6.
(3)∵点D、E在直线l:y1=$\frac{1}{2}$x+1上,
∴设D(p,$\frac{1}{2}$p+1),E(q,$\frac{1}{2}$q+1),其中q>p>0.
如图,过点E作EH⊥DG于点H,则EH=q-p,DH=$\frac{1}{2}$(q-p).
在Rt△DEH中,由勾股定理得:EH2+DH2=DE2,即(q-p)2+[$\frac{1}{2}$(q-p)]2=($\sqrt{5}$)2,
解得q-p=2,即q=p+2.
∴EH=2,E(p+2,$\frac{1}{2}$p+2).
当x=p时,y2=-p2+4p+1,
∴G(p,-p2+4p+1),
∴DG=(-p2+4p+1)-($\frac{1}{2}$p+1)=-p2+$\frac{7}{2}$p;
当x=p+2时,y2=-(p+2)2+4(p+2)+1=-p2+5,
∴F(p+2,-p2+5),
∴EF=(-p2+5)-($\frac{1}{2}$p+2)=-p2-$\frac{1}{2}$p+3.
S四边形DEFG=$\frac{1}{2}$(DG+EF)•EH=$\frac{1}{2}$[(-p2+$\frac{7}{2}$p)+(-p2-$\frac{1}{2}$p+3)]×2=-2p2+3p+3
∴当p=$\frac{3}{4}$时,四边形DEFG的面积取得最大值,
∴D($\frac{3}{4}$,$\frac{11}{8}$)、E($\frac{11}{4}$,$\frac{19}{8}$).
点评 本题是二次函数综合问题,综合考查了二次函数与一次函数的图象与性质、待定系数法、函数最值、勾股定理等知识点,涉及考点众多,难度较大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 某市明天将有80%的时间下雨 | B. | 某市明天将有80%的地区下雨 | ||
| C. | 某市明天一定会下雨 | D. | 某市明天下雨的可能性较大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小鹏早晨到校发现作业忘带,就打电话叫爸爸立即把作业送到学校,小鹏也同时往家赶,两人相遇后,小鹏以原速度返回学校,爸爸则以原速度的$\frac{2}{3}$返回家.设爸爸行走的时间为x分钟,小鹏和爸爸两人之间的距离为y米,y与x的函数关系如图所示,则当小鹏回到学校时,爸爸还需要2.5分钟才能到家.
小鹏早晨到校发现作业忘带,就打电话叫爸爸立即把作业送到学校,小鹏也同时往家赶,两人相遇后,小鹏以原速度返回学校,爸爸则以原速度的$\frac{2}{3}$返回家.设爸爸行走的时间为x分钟,小鹏和爸爸两人之间的距离为y米,y与x的函数关系如图所示,则当小鹏回到学校时,爸爸还需要2.5分钟才能到家.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,矩形ABCD的面积为定值,它的对称中心恰与原点重合,且AB∥y轴,CD交x轴于点M,过原点的直线EF分别交AD、BC边于点E、F,以EF为一边作矩形EFGH,并使EF的对边GH所在直线过点M,若点A的横坐标逐渐增大,图中矩形EFGH的面积的大小变化情况是( )
如图,在平面直角坐标系中,矩形ABCD的面积为定值,它的对称中心恰与原点重合,且AB∥y轴,CD交x轴于点M,过原点的直线EF分别交AD、BC边于点E、F,以EF为一边作矩形EFGH,并使EF的对边GH所在直线过点M,若点A的横坐标逐渐增大,图中矩形EFGH的面积的大小变化情况是( )| A. | 一直减小 | B. | 一直不变 | C. | 先减小后增大 | D. | 先增大后减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com