
���� ��1������ͼ�����ó��𰸣�
��2����С���ӱ��ڰ뾶Ϊr������ӵı��ڰ뾶Ϊ2r����С����ע����Ҫ��ˮ��Ϊ��6��r2����������ˮλ�߶���6cmʱ��Ҫ��ˮ��Ϊ����•��2r��2��6-6��r2=18��r2�����ɵó��𰸣�
��3����x�����������ע��ˮ������ˮ�ڴ��е�ƽ�������ٶ���ȵó����̣��ⷽ�̼��ɣ�
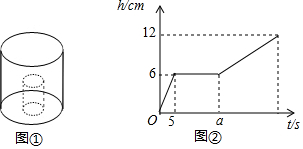
��� �⣺��1������ͼ��֪��С���ӵĸ߶�Ϊ6cm����С����ע��ˮ���õ�ʱ��Ϊ5s�����ӵĸ���С���Ӹߵ�2����
�ʴ�Ϊ��6��5��2��
��2����С���ӱ��ڰ뾶Ϊr������ӵı��ڰ뾶Ϊ2r��
��С����ע����Ҫ��ˮ��Ϊ��6��r2��
��������ˮλ�߶���6cmʱ��Ҫ��ˮ��Ϊ����•��2r��2��6-6��r2=18��r2��
�ߵ�������ˮλ�߶���6cmʱ���õ�ʱ��=5��$\frac{18��{r}^{2}}{6��{r}^{2}}$=15��
����ˮ����Ҫ��ʱ��Ϊ15sʱ����a=15ʱ��������ˮλ�߶���6cm����С���Ӹ߶���ƽ��
��3����x�����������ע��ˮ������ˮ�ڴ��е�ƽ�������ٶ���ȵã�
$\frac{12-6}{x-15}$=$\frac{12}{x}$��
��ã�x=30��
������ó���x=30��ԭ���̵ĸ���
�ʴ�Ϊ��30��
���� ���⿼����һ�κ�����Ӧ�ã�����עˮ���̣�����ע��ˮ�ڴ�ˮ���е������ٶ���ͬ�г������ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 1��$\frac{9}{4}$ | D�� | -1��-$\frac{9}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2 | B�� | y1��y2 | C�� | y1=y2 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Ϊ�˽������ڵİ༶��ÿ��ѧ��������Ь����ȫ��ѧ�������� | |
| B�� | �˽����ǵĻ�����ʶ | |
| C�� | �˽���ӻ�����ܵ�ʹ������ | |
| D�� | ȫ��ѧ����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��3 | B�� | x��-$\frac{2}{3}$��x��3 | C�� | x��-$\frac{2}{3}$ | D�� | x��3��x��-$\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABC��BC����ƽ��2cm�á�DEF�����ı���ABFD���ܳ�Ϊ18cm�����ABC���ܳ�Ϊ��������
��ͼ������ABC��BC����ƽ��2cm�á�DEF�����ı���ABFD���ܳ�Ϊ18cm�����ABC���ܳ�Ϊ��������| A�� | 10 cm | B�� | 12 cm | C�� | 14 cm | D�� | 16 cm |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com