
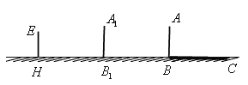
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置![]() ;
;
(2)求路灯灯泡的垂直高度![]() ;
;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1,并求B1C1的长;
【答案】(1)见解析;(2)路灯灯泡的垂直高度GH是4.8m;(3)小明的影子![]() 的长是
的长是![]() m.
m.
【解析】
(1)根据题意,连接CA,HE并延长相交于点G,即为所求路灯灯泡的位置,作出图形即可;
(2)根据题意得到△ABC∽△GHC ,根据相似三角形的性质得到![]() ,代入即可求出答案,
,代入即可求出答案,
(3)与(2)类似得到△![]() ∽△GH
∽△GH![]() ,根据相似三角形的性质推出
,根据相似三角形的性质推出![]() ,代入即可求出答案,连接G
,代入即可求出答案,连接G![]() 延长交HC于点
延长交HC于点![]() ,即得小明的影子.
,即得小明的影子.
(1)如图,连接CA,HE并延长相交于点G,即为所求路灯灯泡的位置,作出图形即可;
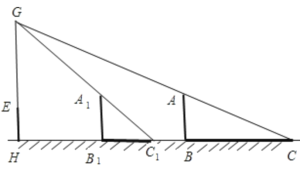
(2)由题意得:易得△ABC∽△GHC,
∴![]() ,
,
∴![]() ,
,
解得:GH=4.8,
答:路灯灯泡的垂直高度GH是4.8m;
故答案为:4.8;
(3)连接G![]() 延长交HC于点
延长交HC于点![]() ,则
,则![]()
![]() 即为小明的影子,在(1)中作图即得,与(2)类似,易证△
即为小明的影子,在(1)中作图即得,与(2)类似,易证△![]() ∽△GH
∽△GH![]() ,
,
∴![]() ,
,
设![]() 长为xm,
长为xm,![]() 为HB的中点,
为HB的中点,
则![]() ,
,
解得:x=![]() ,
,
即![]() =
=![]() m,
m,
答:小明的影子![]() 的长是
的长是![]() m;
m;
故答案为:![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 于点D.
于点D.
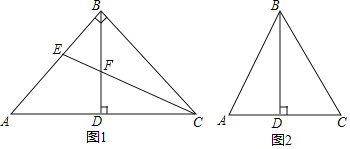
(1)如图1,当![]() 时,若CE平分
时,若CE平分![]() ,交AB于点E,交BD于点F.
,交AB于点E,交BD于点F.
①求证:![]() 是等腰三角形;
是等腰三角形;
②求证:![]() ;
;
(2)点E在AB边上,连接CE.若![]() ,在图2中补全图形,判断
,在图2中补全图形,判断![]() 与
与![]() 之间的数量关系,写出你的结论,并写出求解
之间的数量关系,写出你的结论,并写出求解![]() 与
与![]() 关系的思路.
关系的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图(1),一圆柱的高为5dm,底面半径为5dm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的AC.如下图(2)所示:
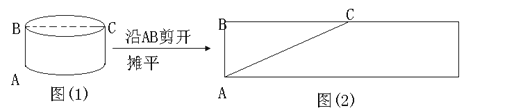
设路线1的长度为![]() ,则
,则![]() ,
,
路线2:高线AB + 底面直径BC.如上图(1)所示:
设路线2的长度为![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1dm,高AB为5dm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:![]() ___________________;
___________________;
路线2:![]() __________
__________
∵![]()
![]() ,
,
∴![]()
![]() (填>或<) 所以应选择路线_________(填1或2)较短.
(填>或<) 所以应选择路线_________(填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 为二次函数
为二次函数![]() 的图象的顶点.
的图象的顶点.
(1)过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,求线段
,求线段![]() 的最小值;
的最小值;
(2)设正比例函数![]() 与上述二次函数的图象相交于点
与上述二次函数的图象相交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
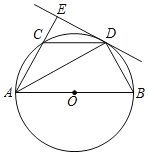
【题目】如图,AB是⊙O的直径,C点在⊙O上,AD平分角∠BAC交⊙O于D,过D作直线AC的垂线,交AC的延长线于E,连接BD,CD.
(1)求证:BD=CD;
(2)求证:直线DE是⊙O的切线;
(3)若DE=![]() ,AB=4,求AD的长.
,AB=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是李老师在黑板上演示的尺规作图及其步骤,
已知钝角![]() ,尺规作图及步骤如下:
,尺规作图及步骤如下:
步骤一:以点![]() 为圆心,
为圆心,![]() 为半径画弧;
为半径画弧;
步骤二:以点![]() 为圆心,
为圆心,![]() 为半径画弧,两弧交于点
为半径画弧,两弧交于点![]() ;
;
步骤三:连接![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.

下面是四位同学对其做出的判断:
小明说:![]() ;
;
小华说:![]() ;
;
小强说:![]() ;
;
小方说:![]() .
.
则下列说法正确的是( )
A.只有小明说得对B.小华和小强说的都对
C.小强和小方说的都不对D.小明和小方说的都对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点(可与
上一点(可与![]() ,
,![]() 重合),以点
重合),以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() (其中
(其中![]() ).
).
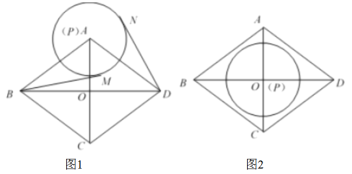
(1)如图1,当点![]() 与
与![]() 重合,且
重合,且![]() 时,过点
时,过点![]() ,
,![]() 分别作
分别作![]() 的切线,切点分别为
的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 与点
与点![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 内部时(不含边界),求
内部时(不含边界),求![]() 的取值范围;
的取值范围;
(3)当点![]() 为
为![]() 或
或![]() 的内心时,直接写出
的内心时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b交x轴于点A(1,0) ,与双曲线![]() 交于点
交于点![]()
(1)求直线AB的解析式为____ ____________;
(2)若 x 轴上存在动点 M(m,0),过点 M 且与 x 轴垂直的直线与直线AB交于点C,与双曲线交于点D(C、D两点不重合),当BC >BD时,写出m的取值范围_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
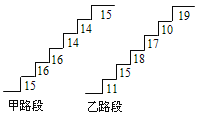
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶,下图是其中的甲、乙两段台阶的示意图,图中的数字表示每一级台阶的高度(单位:cm).请你用所学过的有关统计知识,回答下列问题(数据:15,16,16,14,14,15的方差![]() ,数据:11,15,18,17,10,19的方差
,数据:11,15,18,17,10,19的方差![]() :
:
(1)分别求甲、乙两段台阶的高度平均数;
(2)哪段台阶走起来更舒服?与哪个数据(平均数、中位数、方差和极差)有关?
(3)为方便游客行走,需要陈欣整修上山的小路,对于这两段台阶路.在总高度及台阶数不变的情况下,请你提出合理的整修建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com