
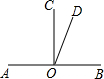
 如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍还大20°,∠AOD比∠BOD的2倍小15°.求∠COD的度数.
如图,直线AB过点O,OC、OD是直线AB同旁的两条射线,若∠BOD比∠COD的3倍还大20°,∠AOD比∠BOD的2倍小15°.求∠COD的度数. 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一块边缘呈抛物线型的铁片如图放置,测得AB=20cm,抛物线顶点到AB边的距离为25cm,现要沿AB边向上依次截取宽度为4cm的矩形铁皮,建立如图所示的直角坐标系.
一块边缘呈抛物线型的铁片如图放置,测得AB=20cm,抛物线顶点到AB边的距离为25cm,现要沿AB边向上依次截取宽度为4cm的矩形铁皮,建立如图所示的直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm,P、Q分别为AB、BC上的动点,点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).
如图,在△ABC中,∠C=90°,AC=3cm,BC=4cm,P、Q分别为AB、BC上的动点,点P从点A出发沿AB方向作匀速移动的同时,点Q从点B出发沿BC方向向点C作匀速移动,移动的速度均为1cm/s,设P、Q移动的时间为t(0<t≤4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当n<0时,m<0 | B. | 当n>0时,m>x2 | C. | 当n<0时,x1<m<x2 | D. | 当n>0时,x2>m>x1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com