
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,则点
,则点![]() 的坐标为____.
的坐标为____.

【答案】(3,-4)
【解析】
将△BOA绕点B顺时针旋转90°得到△BED,可求出D点坐标,DE交x轴于F,连接AD,取AD中点C,连接BC并延长交直线y=-x-1于P,可求出C点坐标,进而可得 直线BC的解析式,由等腰直角三角形的性质可得∠ABC=45°,可得直线BC与直线y=-x-1的交点即为点P,利用方程组求出点P坐标即可.
将线△BOA绕点B顺时针旋转90°得到△BED,DE交x轴于F,连接AD,取AD中点C,连接BC并延长交直线y=-x-1于P,
∵A(6,0),B(0,2),
∴OB=2,OA=6,
∴BE=OB=2,ED=OA=6,AB=BD,∠BED=∠BOA=90°,∠OBE=90°,∠ABD=90°,
∴四边形EFOB是矩形,
∴EF=OB=2,
∴DF=DE-EF=4,
∴D(-2,-4),
∵AB=BD,C为AD中点,∠ABD=90°,
∴∠ABC=45°,
∴直线BC与直线y=-x-1的交点即为点P,
∵A(6,0),D(-2,-4)
∴C(2,-2),
设直线BC的解析式为y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴直线BC的解析式为y=-2x+2,
联立直线BC与直线y=-x-1得:![]() ,
,
解得:![]() ,
,
∴点P坐标为(3,-4).

故答案为:(3,-4)


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】从下列4个函数:①y=3x﹣2;②y=![]() (x<0);③y=
(x<0);③y=![]() (x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
(x>0);④y=﹣x2(x<0)中任取一个,函数值y随自变量x的增大而增大的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥EF,垂足为点E,点H是菱形ABCD的对称中心.若FC=![]() ,EF=
,EF=![]() DE,则菱形ABCD的边长为( )
DE,则菱形ABCD的边长为( )
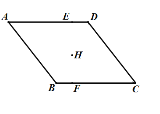
A.![]() B.3C.4D.5
B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=α(0<α<90°),A为OM上一点(不与O重合),点A关于直线ON的对称点为B,AB与ON交于点C,P为直线ON上一点(不与O,C重合)将射线PB绕点P顺时针旋转β角,其中2α+β=180°,所得到的射线与直线OM交于点Q.这个问题中,点的位置和角的大小都不确定,在这里我们仅研究两种特殊情况,一般的情况留给同学们深入探索.
(1)如图1,当α=45°时,此时β=90°,若点P在线段OC的延长线上.
①依题意补全图形;
②求∠PQA﹣∠PBA的值;
(2)如图2,当α=60°,点P在线段CO的延长线上时,用等式表示线段OC,OP,AQ之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2m﹣1)x+m2+1=0.
(1)若方程有实数根,求实数m的取值范围;
(2)设x1,x2分别是方程的两个根,且满足x12+x22=x1x2+10,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
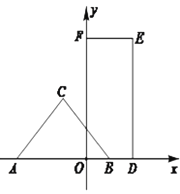
【题目】如图,等腰直角![]() 的斜边
的斜边![]() 在x轴上且长为4,点C在x轴上方.矩形
在x轴上且长为4,点C在x轴上方.矩形![]() 中,点D、F分别落在x、y轴上,边
中,点D、F分别落在x、y轴上,边![]() 长为2,
长为2,![]() 长为4,将等腰直角
长为4,将等腰直角![]() 沿x轴向右平移得等腰直角
沿x轴向右平移得等腰直角![]() .
.
(1)当点![]() 与点D重合时,求直线
与点D重合时,求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() .当线段
.当线段![]() 和线段
和线段![]() 之和最短时,求矩形
之和最短时,求矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积;
重叠部分的面积;
(3)当矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积为
重叠部分的面积为![]() 时,求直线
时,求直线![]() 与y轴交点的坐标.(本问直接写出答案即可)
与y轴交点的坐标.(本问直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
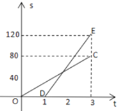
A. 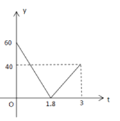 B.
B.  C.
C. 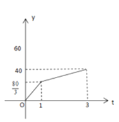 D.
D. 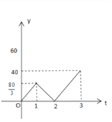
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连结AB,且有AB=DB.
(1)求证:△ADB∽△CDA;
(2)若DB=2,BC=3,求AD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则![]() =__________,
=__________,![]() =_________________ .
=_________________ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com