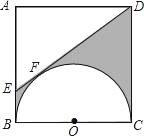
【题目】如图，以正方形ABCD的边BC为直径作半圆O，过点D作直线与半圆相切于点F，交AB于点E，若AB=2cm，则阴影部分的面积为_____．
【答案】
cm2
【解析】分析：由切线长定理可知：BE=EF、DF=DC=2，设AE=xcm，则EF=（2﹣x）cm，故此ED=（4﹣x）cm，然后在Rt△ADE中依据勾股定理列方程求解可求AE的长，再根据阴影部分的面积=正方形的面积﹣△ADE的面积﹣减去半圆的面积计算即可．
详解：由切线长定理可知：BE=EF，DF=DC=2cm．
设AE=xcm，则EF=（2﹣x）cm，ED=（4﹣x）cm．
在Rt△ADE中，AD2+AE2=ED2，即22+x2=（4﹣x）2．
解得：x=1.5．
则AE=1.5cm．
阴影部分的面积=正方形的面积﹣△ADE的面积﹣减去半圆的面积
=2×2﹣
×
×2﹣π×12=
cm2．
故答案为：cm2．
科目：初中数学 来源： 题型：
【题目】八年级380名师生参加户外拓展活动,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表
甲种客车 | 乙种客车 | |
载客量（座/辆） | 60 | 45 |
租金（元/辆） | 550 | 450 |
(1)设租用乙种客车x辆,租车总费用为y元求出y(元)与x(辆)之间的函数表达式;
(2)当乙种客车租用多少辆时,能保障所有的师生能参加户外拓展活动且租车费用最少，最少费用是多少元?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下两个问题，任选其一作答．
如图，OD是∠AOC的平分线，OE是∠BOC的平分线．
问题一：若∠AOC=36°，∠BOC=136°，求∠DOE的度数．
问题二：若∠AOB=100°，求∠DOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】10袋小麦以每袋150干克为准，超过的干克数记为正数，不足的干克数记为负数，分别记为：-6，-3，-1，-2，+7，+3，+4，-3，-2，0.
（1）在这10袋小麦中，最重和最轻的分别重多少干克？
（2）与标准质量相比较，这10袋小麦超过或不足多少干克？
查看答案和解析>>
科目：初中数学 来源： 题型：
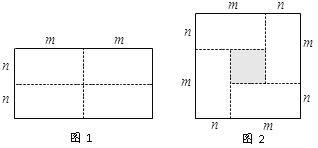
【题目】图1是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的方法拼成一个边长为(m＋n)的正方形．
⑴ 请用两种不同的方法求图2中阴影部分的面积．
方法1： ；方法2： ；
⑵ 观察图2写出
，
，
三个代数式之间的等量关系： ；
⑶ 根据⑵中你发现的等量关系，解决如下问题：若
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
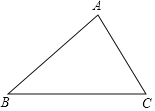
【题目】如图，已知△ABC．利用直尺和圆规，根据下列要求作图（不写作法，保留作图痕迹），并回答问题．
（1）作∠ABC的平分线BD、交AC于点D；
（2）作线段BD的垂直平分线，交AB于点E，交BC于点F，连接DE，DF；
（3）写出你所作出的图形中的相等线段．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB是⊙O的直径，且AB=4，点C在半径OA上（点C与点O、点A不重合），过点C作AB的垂线交⊙O于点D．连接OD，过点B作OD的平行线交⊙O于点E，交CD的延长线于点F．
（1）若点E是
的中点，求∠F的度数；
（2）求证：BE=2OC；
（3）设AC=x，则当x为何值时BEEF的值最大？最大值是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一列数：
，
，
，
，
，
，
，
这串数是由小明按照一定规则写下来的，他第一次写下“，”，第二次接着写“，”，第三次接着写“，”，第四次接着写“，”，沿着这个规则，那么接着“，”后面的三个数应为（ ）
A.
，
，
B.，，
C.
，，
D.，，
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
