
ЁОЬтФПЁПШчЭМЃЌвбжЊABЁЮCDЃЌЕуMЃЌNЗжБ№ЪЧABЃЌCDЩЯСНЕуЃЌЕуGдкABЃЌCDжЎМфЃЎ
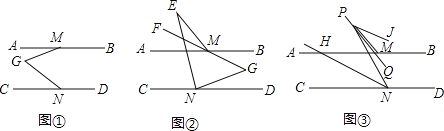
ЃЈ1ЃЉЧѓжЄЃКЁЯAMG+ЁЯCNGЃНЁЯMGNЃЛ
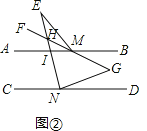
ЃЈ2ЃЉШчЭМЂкЃЌЕуEЪЧABЩЯЗНвЛЕуЃЌMFЦНЗжЁЯAMEЃЌШєЕуGЧЁКУдкMFЕФЗДЯђбгГЄЯпЩЯЃЌЧвNEЦНЗжЁЯCNGЃЌ2ЁЯE+ЁЯGЃН90ЁуЃЌЧѓЁЯAMEЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌШєЕуPЪЧЃЈ2ЃЉжаЕФEMЩЯвЛЖЏЕуЃЌPQЦНЗжЁЯMPQЃЎNHЦНЗжЁЯPNCЃЌНЛABгкЕуHЃЌPJЁЮNHЃЌжБНгаДГіЁЯJPQЕФЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЁЯAMEЃН60ЁуЃЛЃЈ3ЃЉЁЯJPQЃН30ЁуЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуGзїGEЁЮABЃЌЕУГіABЁЮCDЁЮGEЃЌдйгЩЦНааЯпЕФаджЪМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЩшFGгыNEНЛЕуЮЊHЕуЃЌABгыNEЕФНЛЕуIЃЌгЩШ§НЧаЮФкНЧКЭЖЈРэПЩжЊЁЯG+ЁЯHNG+ЁЯNHGЃН180ЁуЃЌдйРћгУНЧЦНЗжЯпЖЈРэЕУГіМД90Ёу+![]() ЁЯAMEЃН180ЁуЃЌМЬЖјЕУГіНсТлЃЛ
ЁЯAMEЃН180ЁуЃЌМЬЖјЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОнPQЦНЗжЁЯMPNЃЌNHЦНЗжЁЯPNCЃЌПЩЕУГіЁЯJPQЃНЁЯJPNЉ![]() ЁЯMPNЃЌгЩДЫЕУГіНсТлЃЎ
ЁЯMPNЃЌгЩДЫЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉжЄУїЃКШчЭМЂйЃЌЙ§ЕуGзїGEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрABЁЮCDЁЮGEЃЌ
ЁрЁЯAMGЃНЁЯMGEЃЌЁЯCNGЃНЁЯNGEЃЌ
ЁрЁЯAMG+ЁЯCNGЃНЁЯMGNЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЩшFGгыNEНЛЕуЮЊHЕуЃЌABгыNEЕФНЛЕуIЃЌ
дкЁїHNGжаЃЌ
ЁпЁЯG+ЁЯHNG+ЁЯNHGЃН180Ёу
ЁрЁЯHNGЃНЁЯAIEЃНЁЯIHM+ЁЯIMHЃНЃЈЁЯE+ЁЯEMFЃЉ+ЁЯIMHЃНЁЯE+ЃЈЁЯEMF+ЁЯIMH ЃЉЃНЁЯE+ЁЯAME
ЁЯNHGЃНЁЯIHMЃНЁЯE+ЁЯEMFЃНЁЯE+![]() ЁЯAME
ЁЯAME
ЁрЁЯG+ЁЯHNG+ЁЯNHGЃНЁЯG+ЃЈЁЯE+ЁЯAMEЃЉ+ЃЈЁЯE+![]() ЁЯAMEЃЉЃН180Ёу ЃЈЁЯG+2ЁЯEЃЉ+
ЁЯAMEЃЉЃН180Ёу ЃЈЁЯG+2ЁЯEЃЉ+![]() ЁЯAMEЃН180ЁуЃЌМД90Ёу+
ЁЯAMEЃН180ЁуЃЌМД90Ёу+![]() ЁЯAMEЃН180ЁуЃЌ
ЁЯAMEЃН180ЁуЃЌ
ЁрЁЯAMEЃН60ЁуЃЛ
ЃЈ3ЃЉЁпPQЦНЗжЁЯMPNЃЌNHЦНЗжЁЯPNCЃЌ
ЁрЁЯJPQЃНЁЯJPNЉ![]() ЁЯMPN
ЁЯMPN
ЃН![]() ЃЈЁЯENCЉ
ЃЈЁЯENCЉ![]() ЁЯMPNЃЉ
ЁЯMPNЃЉ
ЃН![]() ЃЈЁЯAOEЉ
ЃЈЁЯAOEЉ![]() ЁЯMPNЃЉ
ЁЯMPNЃЉ
ЃН![]() ЁЯAME
ЁЯAME
ЃН30ЁуЃЎ


 ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABDЪЧЁбOЕФФкНгШ§НЧаЮЃЌEЪЧЯвBDЕФжаЕуЃЌЕуCЪЧЁбOЭтвЛЕуЃЌЧвЁЯDBCЃНЁЯAЃЌСЌНгOEВЂбгГЄгыЁбOЯрНЛгкЕуFЃЌгыBCЯрНЛгкЕуC.
(1)ЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
(2)ШєЁбOЕФАыОЖЮЊ6ЃЌBCЃН8ЃЌЧѓЯвBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
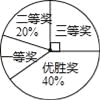
ЁОЬтФПЁПЙњЮёдКАьЙЋЬќдк2015Фъ3дТ16ШеЗЂВМСЫЁЖжаЙњзуЧђЗЂеЙИФИязмЬхЗНАИЁЗЃЌетЪЧжаЙњзуЧђЪЗЩЯЕФжиДѓИФИяЃЌЮЊНјвЛВНЦеМАзуЧђжЊЪЖЃЌДЋВЅзуЧђЮФЛЏЃЌЮвЪаФГЧјдкжааЁбЇОйааСЫЁАзуЧђдкЩэБпЁБжЊЪЖОКШќЃЌИїРрЛёНБбЇЩњШЫЪ§ЕФБШР§ЧщПіШчЭМЫљЪОЃЌЦфжаЛёЕУШ§ЕШНБЕФбЇЩњЙВ50УћЃЌЧыНсКЯЭМжааХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЛёЕУвЛЕШНБЕФбЇЩњШЫЪ§ЃЛ
ЃЈ2ЃЉдкБОДЮжЊЪЖОКШќЛюЖЏжаЃЌAЃЌBЃЌCЃЌDЫФЫљбЇаЃБэЯжЭЛГіЃЌЯжОіЖЈДгетЫФЫљбЇаЃжаЫцЛњбЁШЁСНЫљбЇаЃОйаавЛГЁзуЧђгбвъШќЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓЧЁКУбЁЕНAЃЌBСНЫљбЇаЃЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвджБЯпABЩЯвЛЕуOЮЊЖЫЕузїЩфЯпOCЃЌЪЙЁЯAOCЃН65ЁуЃЌНЋвЛИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕуЗХдкЕуOДІЃЎЃЈзЂЃКЁЯDOEЃН90ЁуЃЉ
ЃЈ1ЃЉШчЭМЂйЃЌШєжБНЧШ§НЧАхDOEЕФвЛБпODЗХдкЩфЯпOAЩЯЃЌдђЁЯCOEЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOЫГЪБеыЗНЯђзЊЖЏЕНФГИіЮЛжУЃЌШєOCЧЁКУЦНЗжЁЯAOEЃЌЧѓЁЯCODЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOШЮвтзЊЖЏЃЌШчЙћODЪМжедкЁЯAOCЕФФкВПЃЌЪдВТЯыЁЯAODКЭЁЯCOEгадѕбљЕФЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌADЪЧИпЃЌBEЪЧжаЯпЃЌCFЪЧНЧЦНЗжЯпЃЌCFНЛADгкGЃЌНЛBEгкHЃЎЯТСаНсТлЃКЂйSЁїABEЃНSЁїBCEЃЛЂкЁЯAFGЃНЁЯAGFЃЛЂлЁЯFAGЃН2ЁЯACFЃЛЂмBHЃНCHЃЎЦфжаЫљгае§ШЗНсТлЕФађКХЪЧ
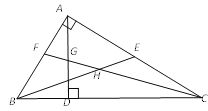
A.ЂйЂкЂлЂмB.ЂйЂкЂлC.ЂкЂмD.ЂйЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦпЃЈвЛЃЉАрЭЌбЇЮЊСЫНтФГаЁЧјМвЭЅдТОљгУЫЎЧщПіЃЌЫцЛњЕїВщСЫИУаЁЧјВПЗжМвЭЅЃЌВЂНЋЕїВщЪ§ОнећРэШчЯТБэЃЈВПЗжЃЉЃКШєИУаЁЧјга ![]() ЛЇМвЭЅЃЌОнДЫЙРМЦИУаЁЧјдТОљгУЫЎСПВЛГЌЙ§
ЛЇМвЭЅЃЌОнДЫЙРМЦИУаЁЧјдТОљгУЫЎСПВЛГЌЙ§ ![]() ЕФМвЭЅдМга
ЕФМвЭЅдМга
|
|
|
|
|
|
|
|
|
| ||
|
|
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊA=3a2b-2ab2+abcЃЌаЁУїЭЌбЇДэНЋЁА2A-BЁБПДГЩЁА2A+BЁБЃЌЫуЕУНсЙћЮЊ4a2b-3ab2+4abcЃЎ
ЃЈ1ЃЉЧѓГі2A-BЕФНсЙћЃЛ
ЃЈ2ЃЉаЁЧПЭЌбЇЫЕЃЈ1ЃЉжаЕФНсЙћЕФДѓаЁгыcЕФШЁжЕЮоЙиЃЌе§ШЗТ№ЃПШєa=![]() ЃЌb=
ЃЌb=![]() ЃЌЧѓЃЈ1ЃЉжаЪНзгЕФжЕЃЎ
ЃЌЧѓЃЈ1ЃЉжаЪНзгЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() СНЕудкЪ§жсЩЯЃЌЕу
СНЕудкЪ§жсЩЯЃЌЕу![]() БэЪОЕФЪ§ЮЊЃ10ЃЌЕу
БэЪОЕФЪ§ЮЊЃ10ЃЌЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыЪЧЕу
ЕФОрРыЪЧЕу![]() ЕНЕу
ЕНЕу![]() ОрРыЕФ3БЖЃЌЕу
ОрРыЕФ3БЖЃЌЕу![]() вдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу
вдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу![]() ЯђгвдЫЖЏ.Еу
ЯђгвдЫЖЏ.Еу![]() вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу
вдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕу![]() ЯђгвдЫЖЏЃЈЕу
ЯђгвдЫЖЏЃЈЕу![]() ЁЂ
ЁЂ![]() ЭЌЪБГіЗЂЃЉ
ЭЌЪБГіЗЂЃЉ
![]()
ЃЈ1ЃЉЪ§жсЩЯЕу![]() ЖдгІЕФЪ§ЪЧ______.
ЖдгІЕФЪ§ЪЧ______.
ЃЈ2ЃЉОЙ§МИУыЃЌЕу![]() ЁЂЕу
ЁЂЕу![]() ЗжБ№ЕНдЕу
ЗжБ№ЕНдЕу![]() ЕФОрРыЯрЕШ.
ЕФОрРыЯрЕШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЪ§жсЩЯЕуAБэЪОЕФгаРэЪ§ЮЊ![]() ЃЌЕуBБэЪОЕФгаРэЪ§ЮЊ6ЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ
ЃЌЕуBБэЪОЕФгаРэЪ§ЮЊ6ЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ![]() дЫЖЏЃЌЭЌЪБЃЌЕуQДгЕуBГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ
дЫЖЏЃЌЭЌЪБЃЌЕуQДгЕуBГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШгЩ![]() дЫЖЏЃЌЕБЕуQЕНДяЕуAЪБPЁЂQСНЕуЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
дЫЖЏЃЌЕБЕуQЕНДяЕуAЪБPЁЂQСНЕуЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() ЕЅЮЛЃКУы
ЕЅЮЛЃКУы![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЪБЃЌЧѓЕуPКЭЕуQБэЪОЕФгаРэЪ§ЃЛ
ЪБЃЌЧѓЕуPКЭЕуQБэЪОЕФгаРэЪ§ЃЛ
ЃЈ2ЃЉЧѓЕуPгыЕуQЕквЛДЮжиКЯЪБЕФtжЕЃЛ
ЃЈ3ЃЉЕБtЕФжЕЮЊЖрЩйЪБЃЌЕуPБэЪОЕФгаРэЪ§гыЕуQБэЪОЕФгаРэЪ§ОрРыЪЧ3ИіЕЅЮЛГЄЖШЃП
![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com