
如果二次函数y=ax2+bx+c的图象的顶点坐标是(2,4),且直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,PQ:QR=1:3,则这个二次函数解析式为 .
y=x2﹣4x+8或y=﹣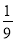 x2+
x2+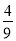 x+
x+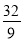 .
.
【解析】
试题分析:根据二次函数y=ax2+bx+c的图象的顶点坐标是(2,4),利用顶点法设该二次函数解析式为y=a(x﹣2)2+4.根据直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,则可确定P点的坐标,并设Q、R点的坐标为(x1,y1)和(x2,y2).根据两点间的距离公式与PQ:QR=1:3求得|x2|与|x1|的比值.直线y=x+4与抛物线相交于Q、R两点列出方程a(x﹣2)2+4=x+4,利用一元二次方程根与系数的关系,可求出x1、x2、a的值.因此抛物线即可确定.
试题解析:∵图象的顶点坐标是(2,4),
∴所以二次函数解析式为y=a(x﹣2)2+4 ①,
∵直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,
∴P点的坐标是(0,4),设Q、R点的坐标为(x1,y1)和(x2,y2),则y1=x1+4,y2=x2+4,
∵|PQ|=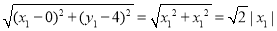 ,
,
|PR|=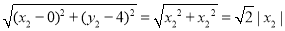 ,
,
∵PQ:QR=1:3且P在QR之处,
∴PQ:PR=PQ:(PQ+QR)=1:4,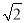 |x1|:
|x1|: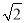 |x2|=1:4,
|x2|=1:4,
∴|x2|=4|x1|②,
又x1,x2是抛物线与直线交点的横坐标,
∴a(x﹣2)2+4=x+4,即ax2﹣(4a+1)x+4a=0,
∴a(x2﹣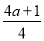 x+4)=0,
x+4)=0,
由韦达定理, ,
,
由③得,x1、x2同号,再由②得 x2=4x1,
∴x1=±1,x2=±4,从④得a=1,或a=﹣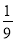
∴y=x2﹣4x+8或y=﹣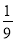 x2+
x2+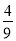 x+
x+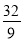 ,
,
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:解答题
在直径是52cm的圆柱形油槽内装入一些油后,截面如图所示,如果油的最大深度CD为16cm,求油面宽度AB的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:选择题
在同一平面直角坐标系中,函数y=kx+2k和函数y=﹣kx2+4x+2(k是常数,且k≠0)的图象可能是( )

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末考试数学试卷(解析版) 题型:解答题
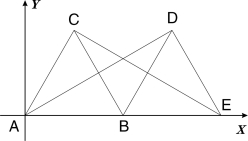
(10分)在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在 轴的正半轴上,连结CE、AD、
轴的正半轴上,连结CE、AD、
(1)求证:AD=CE;
(2)求AD的长;
(3)求过C、E两点的直线的解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市九年级上学期第三次月考数学试卷(解析版) 题型:解答题
如图,△ABC各顶点的坐标分别为A(4、4),B(-2,2),C(3,0),

(1)画出它的以原点O为对称中心的△AˊBˊCˊ;
(2)写出 Aˊ,Bˊ,Cˊ三点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com