
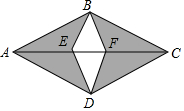
 如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?
如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?  字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AA′,BB′,CC′相交于点O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判断△ABC的面积与△A′B′C′的面积有什么关系?
如图,AA′,BB′,CC′相交于点O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判断△ABC的面积与△A′B′C′的面积有什么关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com