
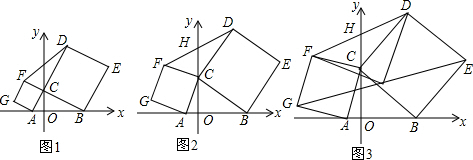
���� ��1����֤��ACB��ֱ�������Σ���֤��FCD�ա�ACB���ɣ�
��2����FJ��y���ڵ�J��DK��y���ڵ�K����֤FJ=OC����֤CHΪAB��һ�룬�Ӷ���CFH������Ϳ�����m��ʾ���������̽�֮���ɣ�
��3��ע������εĶԽ����ƽ�֣��������AF��CG���ڵ�M������CE��BD���ڵ�N������MQ��NQ�����֤��FMQ�ա�QND�������ɵá�DQF�ǵ���ֱ�������Σ�����DQ��FQֵ���䣮
��� �⣺��1����a2+4a+4+b2-16b+64=��a+2��2+��b-8��2=0��
��a=-2��b=8��
��A��-2��0����B��8��0����
��C��0��m����m2=16��
��OC2=OA•OB��
���ACB=90�㣬
���FCD=90�㣬
�ڡ�FCD�͡�ACB�У�
$\left\{\begin{array}{l}{FC=AC}\\{��FCD=��ACB}\\{CD=CB}\end{array}\right.$��
���FCD�ա�ACB��SAS����
��DF=AB��
��2����ͼ2����FJ��y���ڵ�J��DK��y���ڵ�K��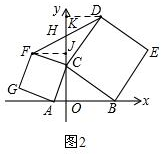
�ߡ�CFJ+��FCJ=��FCJ+��ACO=90�㣬
���CFJ=��ACO��
�ڡ�FCJ�͡�CAO�У�
$\left\{\begin{array}{l}{��CFJ=��ACO}\\{��FJC=��COA}\\{CF=CA}\end{array}\right.$��
���FCJ�ա�CAO��AAS����
��CJ=AO��FJ=CO��
ͬ����DKC�ա�COB��
��DK=CO��CK=BO��
�ڡ�FHJ�͡�DHK�У�
$\left\{\begin{array}{l}{FJ=DK}\\{��FHJ=��DHK}\\{��FJH=��DKH}\end{array}\right.$��
���FHJ�ա�DHK��AAS����
��KH=HJ��
��CH=CJ+JH=AO+$\frac{1}{2}$��CK-CJ��=AO+$\frac{1}{2}$��BO-AO��=$\frac{1}{2}$��AO+BO��=5��
��${S}_{��CFH}=\frac{1}{2}��CH��FJ$=$\frac{1}{2}��m��5=15$��
��m=6��
��C��0��6����
��3������ȷ��
��ͼ3������AF��CG���ڵ�M������CE��BD���ڵ�N������MQ��NQ���ӳ�MQ��BD�ڵ�R��
��CG��AF��������ֱƽ�֣�BD��CE��������ֱƽ�֣�
��QΪEG�е㣬
��MQ��CN��MQ=CN��
NQ��CM��NQ=CM��
��CMQN��ƽ���ı��Σ�
���CMQ=��CNQ��
��FMQ=��QND��
�ڡ�FMQ�͡�QND�У�
$\left\{\begin{array}{l}{FM=QN}\\{��FMQ=��QND}\\{MQ=ND}\end{array}\right.$��
���FMQ�ա�QND��SAS����
���FQM=��QDN��FQ=DQ��
��$\frac{DQ}{FQ}=1$��
���� ���⿼������ȫƽ����ʽ���Ǹ�����Ϊ�㡢���������ε��ж������ʡ������ε����ʡ�ȫ�������ε��ж������ʡ�������������㡢��������λ�ߡ�ƽ���ı��ε��ж������ʵ��ڶ�֪ʶ�㣬�ۺ��Խ�ǿ���ѶȽϴ������ε�һ����Ҫ���ʾ��ǶԽ�����������ֱƽ�֣����������������й��������е���������Ŀ�������ζԽ��ߵĽ�����ǡ���Ȼ�����е㣬�ٺ���֪�е�һ���������Թ�����λ�ߣ��Ӷ��ҵ������ͻ�ƿڣ���һ��Ҫ�μǣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  +4.5 | B�� |  -1.5 | C�� |  -0.4 | D�� |  +0.6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ʮһ��ʮ����ʽ | B�� | ����ʮ����ʽ | C�� | ���ζ���ʽ | D�� | ������ʽ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | û��ʵ���� | ||
| C�� | ��������ȵ�ʵ���� | D�� | ��һ��ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com