
����Ŀ����������Сѧ�����ҵ��й��Ρ������У�ijУ�Բ���ѧ������һ������Ϊ������ϲ����ͼ�顱�ĵ�������ͼ���Ϊ�ס��ҡ����������࣬ѧ���ɸ����Լ��İ�����ѡ����һ��.ѧУ���ݵ������������ͳ�ƣ��������˲�����������ͳ��ͼ������ͳ��ͼ.

������ͼ����Ϣ������������⣺
��1�����ι������� ��ѧ����
��2���������ѧ���У���ϲ������ͼ����� �ˣ���ϲ������ͼ�������ռ���α����������� %��
��3������ϲ������ѧ����ͼ���ѧ���У�Ů������������������1.5����������ѧУ����ѧ��1500�ˣ�������Ƹ�У��ϲ������ͼ���Ů���������ֱ��ж�����.
���𰸡���1��200����2��15��40%����3����ϲ������ͼ���Ů������Ϊ180�ˣ���������Ϊ120��
��������������1���ɱ�����������ռ�İٷֱ�����������ѧ�������ɣ���2������ѧ������������ѧ�������������ռ�İٷֱȼ��ɣ���3�����У��ϲ������ͼ���Ů���������ֱ�1.5x�ˣ�x�ˣ����������г����̣�������̵Ľ⼴�ɵõ������
���������(1)��������ã�40��20%=200(��)��
(2)��������ã�����ѧ����Ϊ200(80+65+40)=15(��)����ϲ������ͼ�������ռ���α�����������![]() ��100%=40%��
��100%=40%��
�� ����������Ϊx�ˣ���Ů������Ϊ1.5x�ˣ����������
x��1.5x��1500��20%
���x��120
��x��120ʱ��1.5x��180
�� ��ϲ������ͼ���Ů������Ϊ180�ˣ���������Ϊ120��


 Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬CD�DZ�AB�ϵĸߣ�
��1����֤����ABC�ס�CBD��
��2�����AC=4��BC=3����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MAN��120�㣬ACƽ�֡�MAN.B��D�ֱ�������AN��AM��.
��1����ͼ1�У�����ABC����ADC=90��ʱ����֤��AD��AB��AC
��2�����ѣ�1���е���������ABC����ADC=90�㡱��Ϊ��ABC����ADC=180���������������䣬��ͼ2��ʾ����1���еĽ����Ƿ���Ȼ�������������������֤����������������˵������.

��ͼ1�� ��ͼ2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������![]() �� ����˵����ȷ���ǣ�������
�� ����˵����ȷ���ǣ�������
A.ͼ���㣨2����1��
B.ͼ��λ�ڵڶ���������
C.��x��0ʱ��y��x���������С
D.��x��0ʱ��y��x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У����Խ���AC���е�O������EF����BC��AD�ֱ�Ϊ��E��F������AE��CF.
(1)��֤���ı���AECF�����Σ�
(2)��AD��8��AB��4����CF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=x+2��˫���� ![]() �ཻ��A��B�������е�A��������Ϊ3����B��������Ϊ��1��
�ཻ��A��B�������е�A��������Ϊ3����B��������Ϊ��1��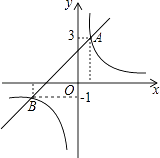
��1����k��ֵ��
��2����y1��y2 �� �������ͼ��ȷ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�Լ��ˮ��ij�й涨����֮��ÿ�±���ˮ��Ϊ15�����ף�����Ϊ1.5Ԫ/�����ף��������ֵ���Ϊ3Ԫ/�����ף�ij����֮�ҵ�����ˮ![]() �����ף�
�����ף�![]() ��Ϊ������
��������
��.������ʽ��ʾ��ˮ![]() �����ķ��ã�
�����ķ��ã�
��.����֮�ҵ��½�ˮ��37.50Ԫ���������˶���������ˮ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������G1��y=ax2+bx+c�Ķ���Ϊ��2����3�����Ҿ����㣨4��1����
��1����������G1�Ľ���ʽ��
��2����������G1������ƽ��3����λ��������ƽ��1����λ��õ�������G2 �� ��������G2��x��ĸ������ཻ��A�㣬��A������ꣻ
��3�����ֱ��m�Ľ���ʽΪ ![]() ����B�ǣ�2����������G2�ϵ�һ���㣬���ڶԳ����Ҳಿ�֣������㣩���˶���ֱ��n����A�͵�B���ʣ��Ƿ���ڵ�B��ʹֱ��m��n��x��Χ�ɵ������κ�ֱ��m��n��y��Χ�ɵ����������ƣ������ڣ������B�����ꣻ�������ڣ���˵�����ɣ�
����B�ǣ�2����������G2�ϵ�һ���㣬���ڶԳ����Ҳಿ�֣������㣩���˶���ֱ��n����A�͵�B���ʣ��Ƿ���ڵ�B��ʹֱ��m��n��x��Χ�ɵ������κ�ֱ��m��n��y��Χ�ɵ����������ƣ������ڣ������B�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݼ���ͼ�ε������ϵ��������ֱ�۵ر�ʾ����ʽ�ij˷������磺(2a+b)(a+b)��2a2+3ab+b2������ͼ(1)��ʾ
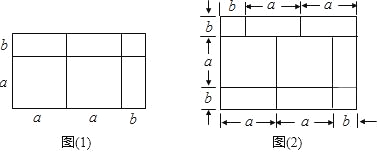
(1)����ͼ(2)��д��һ������ʽ���Զ���ʽ�ĵ�ʽ��
(2)��A��B��������ѡһ������
A���뻭��һ������ͼ�Σ���ʾ(x+p)(x+q)��x2+(p+q)x+pq����������ͼ������Ӧ����ĸ��
B���뻭��һ������ͼ�Σ���ʾ(x��p)(x��q)��x2��(p+q)x+pq����������ͼ������Ӧ����ĸ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com