
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )
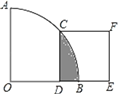
A. 2π﹣8 B. 4π﹣8 C. 2π﹣4 D. 4π﹣4
【答案】C
【解析】试题分析:连接OC,根据C是弧AB的中点,∠AOB=90°,可知∠COB=45°,则有△ODC是等腰直角三角形,再根据勾股定理可求得OC=4;然后根据扇形面积的计算公式可求出S扇形OCB,根据三角形面积的计算公式可求出S△ODC,再根据S阴影=S扇形OCB-S△ODC可求出阴影部分的面积.
解:如图所示,连接OC:

∵C是弧AB的中点,∠AOB=90°,
∴∠COB=45°.
∵四边形CDEF是正方形,且其边长为2![]() ,
,
∴∠ODC=90°,CD=2![]() ,
,
∴在Rt△ODC中,OD=CD=2![]() ,OC=
,OC=![]() =4,
=4,
∴S扇形OCB=![]() ·π·42=2π,S△ODC=
·π·42=2π,S△ODC=![]() OD·CD=4,
OD·CD=4,
∴S阴影=S扇形OCB-S△ODC=2π-4.
故选C.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题: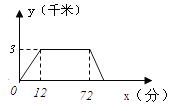
(1)小明家离超市的距离是千米;
(2)小明在超市买东西时间为小时;
(3)小明去超市时的速度是千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
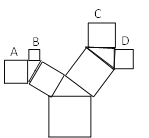
【题目】如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是 _____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.
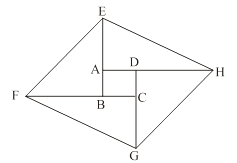
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com