
分析 先将代数式($\frac{1}{a+2}$-$\frac{1}{a-2}$)÷$\frac{1}{a-2}$进行化简,然后将a=3代入求解即可.
解答 解:($\frac{1}{a+2}$-$\frac{1}{a-2}$)÷$\frac{1}{a-2}$
=($\frac{a-2}{{a}^{2}-4}$-$\frac{a+2}{{a}^{2}-4}$)÷$\frac{1}{a-2}$
=(-$\frac{4}{{a}^{2}-4}$)×(a-2)
=-$\frac{4}{a+2}$.
当a=3时,
原式=-$\frac{4}{3+2}$=-$\frac{4}{5}$.
点评 本题考查了分式的化简求值,解答本题的关键在于先将代数式($\frac{1}{a+2}$-$\frac{1}{a-2}$)÷$\frac{1}{a-2}$进行化简,然后将a=3代入求解.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
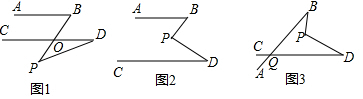
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
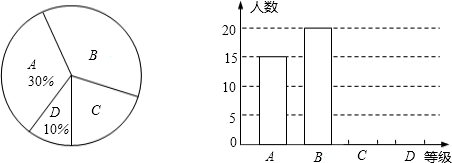
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E | 职员F | 职员G |
| 月工资/元 | 12000 | 8000 | 3200 | 2600 | 2400 | 2200 | 2200 | 2200 | 1200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
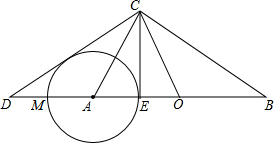 如图,在△ABC与△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
如图,在△ABC与△OCD中,∠ACB=∠DCO=90°,O为AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
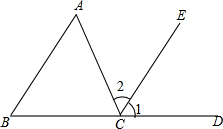 如图,已知CE∥BA,并且点B、C、D三点在同一直线上,你能利用平行线的性质去说明∠A+∠B+∠ACB=180°吗?由此你能归纳出关于三角形三个内角之和的特性吗?
如图,已知CE∥BA,并且点B、C、D三点在同一直线上,你能利用平行线的性质去说明∠A+∠B+∠ACB=180°吗?由此你能归纳出关于三角形三个内角之和的特性吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com