
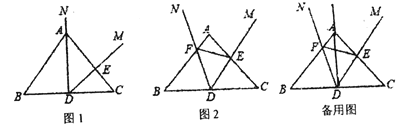
【题目】问题情境:在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,以
的中点,以![]() 为角的顶点作
为角的顶点作![]() .
.
感知易证:(1)如图1,当射线![]() 经过点
经过点![]() 时,
时,![]() 交边
交边![]() 于点
于点![]() .将
.将![]() 从图1中的位置开始,绕点
从图1中的位置开始,绕点![]() 按逆时针方向旋转,使射线
按逆时针方向旋转,使射线![]() 、
、![]() 始终分别交边
始终分别交边![]() ,
,![]() 于点
于点![]() 、
、![]() ,如图2所示,易证
,如图2所示,易证![]() ,则有
,则有![]() .
.
操作探究:(2)如图2,![]() 与
与![]() 是否相似,若相似,请证明;若不相似,请说明理由;
是否相似,若相似,请证明;若不相似,请说明理由;
拓展应用:(3)若![]() ,直接写出当(2)中的旋转角为多少度时,
,直接写出当(2)中的旋转角为多少度时,![]() 与
与![]() 相似.
相似.
【答案】(1)CD;(2)△BDF∽△DEF,理由见详解;(3)10°或40°.
【解析】
(1)如图2,根据∠EDF=∠B及三角形外角性质可得∠BFD=∠CDE,再根据∠B=∠C即可得到△BFD∽△CDE解决问题.
(2)如图2,由(2)得△BFD∽△CDE,则有![]() ,由D是BC的中点可得
,由D是BC的中点可得![]() .再根据∠B=∠EDF即可得到△BDF∽△DEF.
.再根据∠B=∠EDF即可得到△BDF∽△DEF.
(3)由∠B=∠C=50°可得∠BAC=80°,AB=AC,再由BD=CD可得AD⊥BC.若△DEF与△ABC相似,由△BDF∽△DEF可得△BDF与△ABC相似,从而得到∠BDF=∠BAC=80°,或∠BDF=∠C=50°,即可解决问题.
解:(1)如图2,
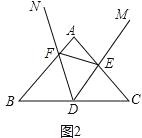
∵AB=AC
∴∠B=∠C,
∵∠FDC是△BFD的一个外角,
∴∠FDC=∠B+∠BFD.
∵∠FDC=∠FDE+∠EDC,∠EDF=∠B,
∴∠BFD=∠CDE.
∵∠B=∠C,
∴△BFD∽△CDE;
∴![]() .
.
(2)如图2,结论:△BDF∽△DEF.

理由:由(1)得![]() .
.
∵D是BC的中点,
∴BD=CD,
∴![]() ,
,
又∵∠B=∠EDF,
∴△BDF∽△DEF.
(3)连接AD,如图3,
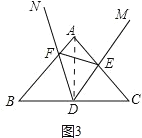
∵∠B=∠C=50°,
∴∠BAC=80°,AB=AC.
∵BD=CD,
∴AD⊥BC.
若△DEF与△ABC相似,
∵△BDF∽△DEF,
∴△BDF与△ABC相似,
∴∠BDF=∠BAC=80°,或∠BDF=∠C=50°,
∴∠ADF=90°﹣80°=10°,或∠ADF=90°﹣50°=40°,
∴当(2)中的旋转角为10°或40°时,△DEF与△ABC相似.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如果点
中,如果点![]() ,点
,点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 的“伴随菱形”,下图为点
的“伴随菱形”,下图为点![]() 的“伴随菱形”的一个示意图.
的“伴随菱形”的一个示意图.
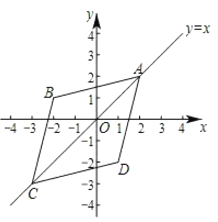
已知点![]() 的坐标为(1,1),点
的坐标为(1,1),点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 中,能够成为点
中,能够成为点![]() 的“伴随菱形”的顶点的是__________________;
的“伴随菱形”的顶点的是__________________;
(2)如果四边形![]() 是点
是点![]() 的“伴随菱形”.
的“伴随菱形”.
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
②当四边形![]() 中较小内角的度数为60°时,求四边形
中较小内角的度数为60°时,求四边形![]() 的面积;
的面积;
③当四边形![]() 的面积为8,且与直线
的面积为8,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
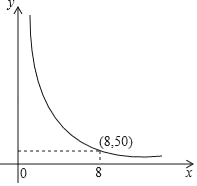
【题目】码头工人每天往一艘轮船上装载货物,平均每天装载速度y(吨/元)与装完货物所需时间x(天)之间是反比例函数关系,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)由于紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸货多少吨?
(3)若码头原有工人10名,且每名工人每天的装卸量相同,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算x[]y=![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=![]() =﹣2b.已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
=﹣2b.已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
(1)求a,b的值;
(2)若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
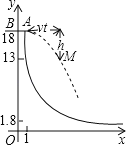
【题目】如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=![]() (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
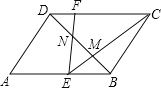
①E为AB的中点;
②FC=4DF;
③S△ECF=![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,4),B(1,2),C(5,1)是平面直角坐标系中的三点.
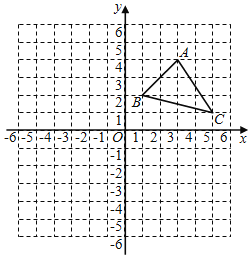
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标;
(3)连接AA1,BB1,求四边形AA1B1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
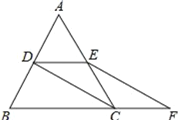
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com