
【题目】如图,AB是⊙O的直径,弦DE垂直半径OA,C为垂足,DE=6,连接DB,![]() ,过点E作EM∥BD,交BA的延长线于点M.
,过点E作EM∥BD,交BA的延长线于点M.

(1)求的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45°时,求图中阴影部分的面积.
【答案】⑴ OE=2![]() ;⑵ 见详解 ⑶
;⑵ 见详解 ⑶![]()
【解析】
(1) 连结OE,根据垂径定理可以得到![]() ,得到∠AOE =60,OC=
,得到∠AOE =60,OC=![]() OE,根据勾股定理即可求出.
OE,根据勾股定理即可求出.
(2) 只要证明出∠OEM=90°即可,由(1)得到∠AOE =60,根据EM∥BD,∠B=∠M=30°,即可求出.
(3) 连接OF,根据∠APD=45°,可以求出∠EDF=45,根据圆心角为2倍的圆周角,得到∠BOE,用扇形OEF面积减去三角形OEF面积即可.
(1)连结OE
∵DE垂直OA,∠B=30°∴CE=![]() DE=3,
DE=3,![]()
∴∠AOE=2∠B=60,∴∠CEO=30°,OC=![]() OE
OE
由勾股定理得OE=![]()
(2) ∵EM∥BD,
∴∠M=∠B=30,∠M+∠AOE=90
∴∠OEM=90,即OE⊥ME,
∴EM是⊙O的切线
(3)再连结OF,当∠APD=45时,∠EDF=45, ∴∠EOF=90
S阴影=![]() =
=![]()


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,以O为圆心,以任意长为半径作弧,交OA,OB于点M,N,分别以点M,N为圆心,以大于![]() MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
MN的长度为半径作弧,两弧在∠AOB内交于点P,以OP为边作∠POC=15°,则∠BOC的度数为( )
A.15°B.45°C.15°或30°D.15°或45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 汕头国际马拉松赛事设有“马拉松(
汕头国际马拉松赛事设有“马拉松(![]() 公里)”,“半程马拉松(
公里)”,“半程马拉松(![]() 公里)”,“迷你马拉松(
公里)”,“迷你马拉松(![]() 公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小红被分配到“马拉松(![]() 公里)”项目组的概率为___________.
公里)”项目组的概率为___________.
(2)用树状图或列表法求小红和小青被分到同一个项目组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,∠ADB=∠AEC=90°,∠ABD=∠ACE=30°,连接DE.若DE=5,则BC长为_____.
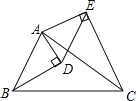
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a、b、c是常数,a<0)经过点A(-1,0)、B(3,0),顶点为C,则下列说法正确的个数是( )
①当-1<x<3时,ax2+bx+c>0;②当△ABC是直角三角形,则a=-![]() ;
;
③若m≤x≤m+3时,二次函数y=ax2+bx+c的最大值为am2+bm+c,则m≥3.
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4张卡片,分别印有数字1、2、3、6,这4张卡片除印有的数字不同外,其余都相同.
(1)搅匀后从中任意摸出1张卡片,摸到印有奇数卡片的概率为_______;
(2)搅匀后从中任意摸出1张卡片,将该卡片印有的数字记为![]() ,再从剩余3张卡片中任意摸出1张卡片,将该卡片印有的数字记为
,再从剩余3张卡片中任意摸出1张卡片,将该卡片印有的数字记为![]() ,请用列表或画树状图的方法求出点
,请用列表或画树状图的方法求出点![]() 在反比例函数
在反比例函数![]() 图像上的概率.
图像上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=4,点P在边BC上,联结AP,将△ABP绕着点A旋转,使得点P与边AC的中点M重合,点B的对应点是点B′,则BB′的长等于_____.
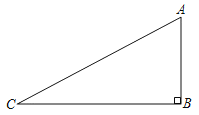
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
(1)求证:CD是⊙O的切线;
(2)若BC=3,AB=5,求平行四边形OABC的面积.
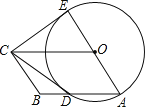
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在地面A处利用测角仪观测气球C的仰角为37°,然后他沿正对气球方向前进了40m到达地面B处,此时观测气球的仰角为45°.求气球的高度是多少?参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75
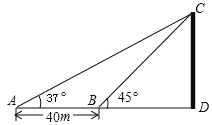
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com