
【题目】如下图,已知⊙O的直径为AB,AC⊥AB于点A, BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.下面四个结论:①ED是⊙O的切线;②BC=2OE③△BOD为等边三角形;④△EOD ∽ △CAD,正确的是( )
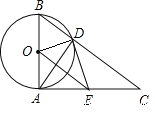
A. ①② B. ②④ C. ①②④ D. ①②③④
【答案】C
【解析】解:如图,连接OD.∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°.在△AOE与△DOE中,∵OA=OD,AE=DE,OE=OE,∴△AOE≌△DOE(SSS),∴∠OAE=∠ODE=90°,即OD⊥ED.又∵OD是⊙O的半径,∴ED是⊙O的切线.故①正确;
∵△AOE≌△DOE,∴∠AOE=∠DOE,∵OB=OD,∴∠B=∠BDO,∵∠B+∠BDO=∠AOE+∠DOE,∴∠B=∠AOE,∴OE∥BC,∵AO=OB,∴OE是△BAC的中位线,∴BC=2OE,故②正确;
∵OE∥BC,∴∠AEO=∠C.∵△AOE≌△DOE,∴∠DEO=∠C,∠ODE=∠OAE=90°,∴∠ODE=ADC=90°,∴△EOD∽△CAD,∴正确的①②④.故选C.


科目:初中数学 来源: 题型:
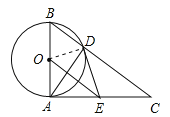
【题目】在△ABC中,∠ACB=90°,点D、E分别在边BC、AC上,AC=3AE,∠CDE=45°(如图),△DCE沿直线DE翻折,翻折后的点C落在△ABC内部的点F,直线AF与边BC相交于点G,如果BG=AE,那么tanB=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为x=1,与y轴的交点B在(0,2)和(0,3)之间(包含这两个点)运动.有如下四个结论:①抛物线与x轴的另一个交点是(3,0);②点C(x1,y1),D(x2,y2)在抛物线上,且满足x1<x2<1,则y1>y2;③常数项c的取值范围是2≤c≤3;④系数a的取值范围是﹣1≤a≤﹣![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
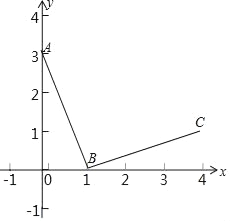
【题目】如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y=![]() 的图象G经过点C.
的图象G经过点C.
(1)请直接写出点C的坐标及k的值;
(2)若点P在图象G上,且∠POB=∠BAO,求点P的坐标;
(3)在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连接AD.
(1)求证:AD=AN;
(2)若AB=8,ON=1,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
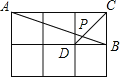
【题目】如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结CD与AB相交于点P,则tan∠APD的值是( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:①都是直角三角形;②都是锐角三角形;③都是钝角三角形.
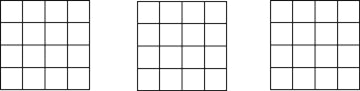
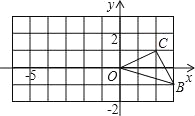
(2)如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
①以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
②分别写出B、C两点的对应点B′、C′的坐标;
③如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com