练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．近年来，全国房价不断上涨，某市201 4年4月份的房价平均每平方米为6600元，比2012年同期的房价平均每平方米上涨了2000元，假设这两年该市房价的平均增长率均为x，则关于x的方程为（　　）
    A．（1+x）2=2000B．2000（1+x）2=6600
    C．（6600-200）（1+x）=6600D．（6600-2000）（1+x）2=6600

    分析 设这两年该县房价的平均增长率均为x，那么2013年4月份的房价平均每平方米为（5600-2000）（1+x）元，2014年4月份的房价平均每平方米为（6600-2000）（1+x）（1+x）元，然后根据某县2014年4月份的房价平均每平方米为6600元即可列出方程．

    解答 解：∵某县2014年4月份的房价平均每平方米为6600元，比2012年同期的房价平均每平方米上涨了2000元，
    ∴2012年同期的房价平均每平方米4600元，假设这两年该县房价的平均增长率均为x，
    则关于x的方程为：（6600-2000）（1+x）2=6600．
    故选D．

    点评 本题考查了求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．阅读材料（1），并利用（1）的结论解决问题（2）和问题（3）．
    （1）如图1，AB∥CD，E为形内一点，连结BE、DE得到∠BED，求证：∠E=∠B+∠D．
    悦悦是这样做的：
    过点E作EF∥AB．则有∠BEF=∠B．
    ∵AB∥CD，∴EF∥CD．
    ∴∠FED=∠D．
    ∴∠BEF+∠FED=∠B+∠D．
    即∠BED=∠B+∠D．
    （2）如图2，画出∠BEF和∠EFD的平分线，两线交于点G，猜想∠G的度数，并证明你的猜想．
    （3）如图3，EG1和EG2为∠BEF内满足∠1=∠2的两条线，分别与∠EFD的平分线交于点G1和G2，求证：∠FG1E+∠G2=180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在两个半圆中，大圆的弦MN与小圆相切，D为切点，且MN∥AB，MN=a，ON、CD分别为两圆的半径，求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列是二元一次方程的是（　　）
    A．3x-6=xB．3x=2yC．2x+$\frac{3}{y}$=1D．2x-3y=xy

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．分式方程$\frac{2x}{x-1}$=3的解为（　　）
    A．x=4B．x=3C．x=2D．x=-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．m为正整数，已知二元一次方程组$\left\{\begin{array}{l}{mx+2y=10}\\{3x-2y=0}\end{array}\right.$有整数解，则m2的值为（　　）
    A．4B．49C．4或49D．1或49

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．方程x2+4x-6=0配方后变形为（　　）
    A．（x+2）2=10B．（x-2）2=10C．（x+2）2=2D．（x-2）2=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．函数y=kx+b的图象由函数y=-2x+1平移得到，且过点（1，3），则函数关系式为y=-2x+5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

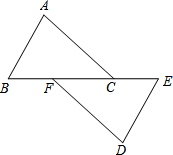    4．如图，已知点B、F、C、E在同一直线上，AB∥DE，AB=DE，BF=EC，试说明AC与DF平行的理由．
    解：因为AB∥DE（已知），
    所以∠B=∠E（两直线平行，内错角相等）．
    因为 BF=EC（已知），
    所以BF+FC=EC+CF（等式性质），
    即 BC=EF．
    在△ABC和△DEF中，$\left\{\begin{array}{l}AB=DE（已知）\\∠B=∠E（已证）\\ BC=EF（已证）\end{array}\right.$
    所以△ABC≌△DEF． （SAS）
    所以∠ACB=∠DFE（全等三角形的对应角相等），
    所以AC∥DF内错角相等，两直线平行．

    查看答案和解析>>

    同步练习册答案