
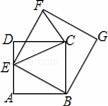
如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为 .


 .
.
【考点】正方形的性质.
【分析】过点F作FM⊥AD延长线于点M,令EF与CD的交点为N点,设AE=x.根据三角形的面积公式可知S△CEF=
 CN•ME,由此可知当CN最小时△CEF的面积取最小值.根据给定的条件已经角的计算找出“∠AEB=∠MFE,∠ABE=∠MEF”,从而证出△ABE≌△MEF,即得出MF=AE,ME=AB,再通过相似三角形的性质用含x的关系式表示出DN的长度,根据二项式的性质即可找出DN的最大值,将其代入前面的面积公式中即可得出结论.
CN•ME,由此可知当CN最小时△CEF的面积取最小值.根据给定的条件已经角的计算找出“∠AEB=∠MFE,∠ABE=∠MEF”,从而证出△ABE≌△MEF,即得出MF=AE,ME=AB,再通过相似三角形的性质用含x的关系式表示出DN的长度,根据二项式的性质即可找出DN的最大值,将其代入前面的面积公式中即可得出结论.
【解答】解:过点F作FM⊥AD延长线于点M,令EF与CD的交点为N点,如图所示.


则S△CEF=
 CN•ME.
CN•ME.
∵四边形ABCD为正方形,四边形BEFG为正方形,
∴∠A=90°,∠BEF=90°,BE=EF,
∴∠AEB+∠ABE=90°,∠MEF+∠MFE=90°,∠AEB+∠BEF+∠MEF=180°,
∴∠AEB=∠MFE,∠ABE=∠MEF.
在△ABE和△MEF中,

 ,
,
∴△ABE≌△MEF(ASA).
∴MF=AE,ME=AB.
∵CD⊥AD,FM⊥AD,
∴ND∥FM,
∴△EDN∽△AMF,
∴
 .
.
设AE=x,则ED=AD﹣AE=2﹣x,EM=AB=2,MF=AE=x,
∴DN=
 =﹣x2+x=﹣
=﹣x2+x=﹣
 (x﹣1)2+
(x﹣1)2+
 ≤
≤
 .
.
∴CN=CD﹣DN≥2﹣
 ≥
≥
 .
.
∴△CEF面积的最小值为
 CN•ME=
CN•ME=
 ×
×
 ×2=
×2=
 .
.
故答案为:
 .
.
【点评】本题考查了正方形的性质、全等三角形的判定及性质、相似三角形的判定及性质、三角形的面积公式及二次函数的性质,解题的关键是找出线段DN的最大值.本题属于中档题,难度不大,解决该题型题目时,根据三角形的面积公式找出其去最值的条件,再结合二次函数的性质去解决最值问题.


科目:初中数学 来源: 题型:
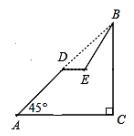
如图,已知斜坡 AB 长为 60 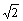 米,坡角(即∠BAC)为 45º, BC⊥ AC.现计划在斜坡中点 D 处挖去部分斜坡,修建一个平行于水平线 AC 的休闲平台 DE 和一条新的斜坡 BE ,若修建的斜坡 BE 的坡比为
米,坡角(即∠BAC)为 45º, BC⊥ AC.现计划在斜坡中点 D 处挖去部分斜坡,修建一个平行于水平线 AC 的休闲平台 DE 和一条新的斜坡 BE ,若修建的斜坡 BE 的坡比为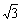 :1 ,求休闲平台 DE 的长是多少米?(结果保留根号).
:1 ,求休闲平台 DE 的长是多少米?(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
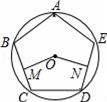

A.108° B.144° C.150° D.166°
查看答案和解析>>
科目:初中数学 来源: 题型:
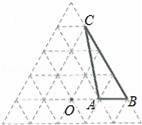
如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
为了掌握某次数学模拟考试卷的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
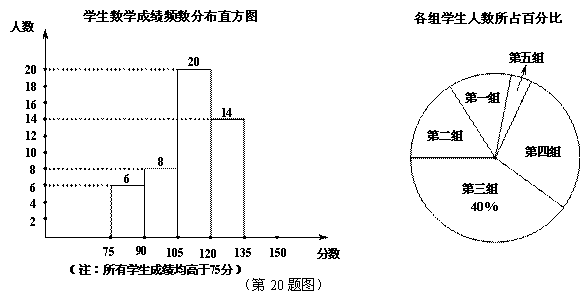 |
请将频数分布直方图补充完整;若老师找到第五组中一个学生的语文、数学、英语三科成绩,如下表.老师将语文、数学、英语成绩按照3:5:2的比例给出这位同学的综合分数.求此同学的综合分数.
| 科目 | 语文 | 数学 | 英语 |
| 得分 | 120 | 146 | 140 |
查看答案和解析>>
科目:初中数学 来源:2015-2016学年江苏省七年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,是由7个棱长都为1的小正方体组合成的简单几何体.
(1)该几何体的表面积(含下底面)为 ;
(2)请画出这个几何体的三视图;
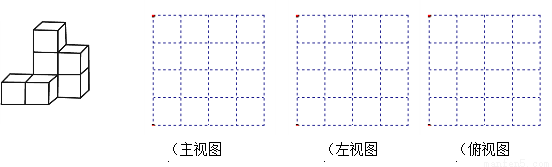
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com