
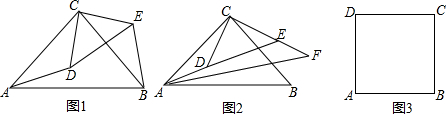
���� ��1������������нǶ�Ӧ��ȵ�����������ȫ�ȼ����жϣ�
��2�����ۣ�AB-DE=$\sqrt{2}$EF������֤��CA=CF���ٸ���EF=CF-CE=CA-CE����$\sqrt{2}$EF=$\sqrt{2}$CA-$\sqrt{2}$CE���ɴ˼���֤����
��3����ͼ3�У���DΪԲ��1Ϊ�뾶����D������B����D������BP��BP�䣬����BD����AE��BP����E��AF��BP��F�����BE��AF���ɽ�����⣮
��� ��1��֤������ͼ1�У�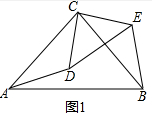
�ߡ�ACB=��DCE=90�㣬
���ACD=��BCE��
�ڡ�ACD�͡�BCE�У�
$\left\{\begin{array}{l}{AC=CB}\\{��ACD=��BCE}\\{CD=CE}\end{array}\right.$��
���ACD�ա�BCE��
��2�����ۣ�AB-DE=$\sqrt{2}$EF��
���ɣ���ͼ2�У�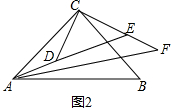
��CD=CE����DCE=90�㣬
���CED=45�㣬DE=$\sqrt{2}$CE��
��CA=CB����ACB=90�㣬
���CAB=45�㣬AB=$\sqrt{2}$CA��
�ߡ�CED=��F+��EAF��
���F=45��-��EAF��
�ߡ�CAF=��CAB-��FAB=45��-��FAB��
�ߡ�EAF=��FAB��
���CAF=��F��
��CA=CF��
��EF=CF-CE=CA-CE��
��$\sqrt{2}$EF=$\sqrt{2}$CA-$\sqrt{2}$CE=AB-DE��
��AB-DE=$\sqrt{2}$EF��
��3����ͼ3�У���DΪԲ��1Ϊ�뾶����D������B����D������BP��BP�䣬����BD����AE��BP����E��AF��BP��F��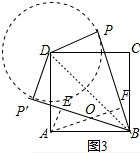
���ı���ABCD�������Σ�CD=BC=AB=AD=$\sqrt{2}$��
��BD=$\sqrt{2}$DC=2����ABC=90�㣬
��Rt��PBD�У��ߡ�BPD=90�㣬BD=2��DP=1��
���PBD=30�㣬ͬ����P��BD=30�㣬
���ABE=��CBP=15�㣬
�ڡ�ABE�͡�BAF�У�
$\left\{\begin{array}{l}{��AEB=��AFB}\\{��EAB=��FBA=75��}\\{AB=BA}\end{array}\right.$��
���ABE�ա�BAF��
���ABE=��OAB=15�㣬
���AOE=��FOB=30�㣬
��AO=OB=2AE����AE=a����AO=OB=2a��EO=$\sqrt{3}$a��
��EB=AF=2a+$\sqrt{3}$a��
��AB2=AE2+BE2��
��2=a2+��2a+$\sqrt{3}$a��2��
��a=$\frac{\sqrt{3}-1}{2}$�������Ѿ���������
��AE=$\frac{\sqrt{3}-1}{2}$��AF=BE=2a+$\sqrt{3}$a=$\frac{\sqrt{3}+1}{2}$��
�ʴ�Ϊ$\frac{\sqrt{3}-1}{2}$��$\frac{\sqrt{3}+1}{2}$��
���� ���⿼���ı����ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����Բ��֪ʶ������Ĺؼ������������Щ֪ʶ��ѧ������Բ�����ߵ����ʽ�����⣬�����п�ѹ���⣮


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
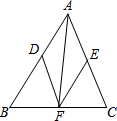 ��ABC�У�DF��AC��EF��AB��AFƽ�֡�BAC��
��ABC�У�DF��AC��EF��AB��AFƽ�֡�BAC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
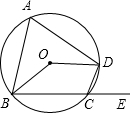 ��ͼ���ı���ABCD�ڽ��ڡ�O������BOD=138�㣬������һ����ǡ�DCE����69�㣮
��ͼ���ı���ABCD�ڽ��ڡ�O������BOD=138�㣬������һ����ǡ�DCE����69�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com