练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在Rt△ABC中，斜边AB=5，而直角边BC，AC之长是一元二次方程x2-（2m-1）x+4（m-1）=0的两根，则m的值是（ ）

    A. 4 B. -1 C. 4或-1 D. -4或1

    【答案】A

    【解析】

    利用一元二次方程根与系数的关系，求出a+b和ab，利用勾股定理可得出a2+b2=25，再将方程左边转化为（a+b）2-2ab，然后整体代入建立关于m的方程，解方程求出m的值，再由a+b＞0，确定m的值。

    如图．设BC=a，AC=b．根据题意得a+b=2m-1，ab=4（m-1）．
    由勾股定理可知a2+b2=25，
    ∴a2+b2=（a+b）2-2ab=（2m-1）2-8（m-1）=4m2-12m+9=25，
    ∴4m2-12m-16=0，
    即m2-3m-4=0，
    解之得m1=-1，m2=4．
    ∵a+b=2m-1＞0，
    即m＞ ，
    ∴m=4．
    故答案为：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

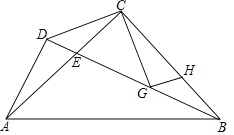
    【题目】如图△ABC中，CA＝CB，∠ACB＝90°，D为△ABC外一点，且AD⊥BD，BD交AC于E，G为BC上一点，且∠BCG＝∠DCA，过G点作GH⊥CG交CB于H．

    （1）求证：CD＝CG；

    （2）若AD＝CG，求证：AB＝AC+BH．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于抛物线.

    （1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；

    （2）在坐标系中利用描点法画出此抛物线；

    x

    …






    …

    y

    …






    …

    （3）利用以上信息解答下列问题：若关于x的一元二次方程（t为实数）在＜x＜的范围内有解，则t的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰中，，在中，，与交于点。

    （1）如图1，若，求的长；

    （2）如图2，为延长线上一点，连接，若，求证：。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】菱形ABCD的边长为4cm,∠A=120°，则菱形ABCD的面积为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按指定的方法解下列方程：

    （1）2x2-5x-4=0（配方法）；

    （2）3（x-2）+x2-2x=0（因式分解法）；

    （3）（a2-b2）x2-4abx=a2-b2（a2≠b2）（公式法）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解

    如图1，△ABC中，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，剪掉重复部分；…；将余下部分沿∠BnAnC的平分线AnBn+1折叠，点Bn与点C重合，无论折叠多少次，只要最后一次恰好重合，∠BAC是△ABC的好角．

    小丽展示了确定∠BAC是△ABC的好角的两种情形．情形一：如图2，沿等腰三角形ABC顶角∠BAC的平分线AB1折叠，点B与点C重合；情形二：如图3，沿∠BAC的平分线AB1折叠，剪掉重复部分；将余下部分沿∠B1A1C的平分线A1B2折叠，此时点B1与点C重合．

    探究发现

    △ABC中，∠B=2∠C，经过两次折叠，∠BAC是不是△ABC的好角？ 　 　（填“是”或“不是”）．

    小丽经过三次折叠发现了∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为 ．

    根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为　 　．

    应用提升

    （3）小丽找到一个三角形，三个角分别为15°、60°、105°，发现60°和105°的两个角都是此三角形的好角．

    请你完成，如果一个三角形的最小角是4°，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A（4,0），点B（0,6），点P是直线AB上的一个动点，已知点P的坐标为（m,n）.

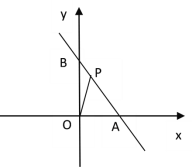
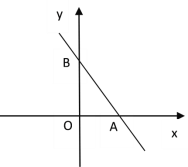
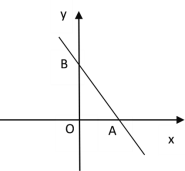
    (1)当点P在线段AB上时（不与点A、B重合）

    ①当m=2,n=3时，求△POA的面积.

    ②记△POB的面积为S，求S关于m的函数解析式，并写出定义域.

    （2）如果S△BOP：S△POA=1:2,请直接写出直线OP的函数解析式.（本小题只要写出结果，不需要写出解题过程）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α等于(　　)

    A. 20° B. 30° C. 40° D. 50°

    查看答案和解析>>

    同步练习册答案