
【题目】如图,在等边△ABC中,DE分别是边AB、AC上的点,且AD=CE,则∠ADC+∠BEA=( )
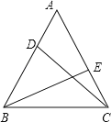
A.180°B.170°C.160°D.150°
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】体育器材室有A、B两种型号的实心球,1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克.
(1)每只A型球、B型球的质量分别是多少千克?
(2)现有A型球、B型球的质量共17千克,则A型球、B型球各有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE,CG平分∠ACB交BD于点G,
(1)如图1,求证:CF=BG;
(2)如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
求证:PB=CP+CF;
(3)如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3![]() ,BG=6,求AC的长.
,BG=6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了创建书香校园,去年又购进了一批图书.经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.
(1)求去年购进的文学羽和科普书的单价各是多少元?
(2)若今年文学书和科普书的单价和去年相比保持不变,该校打算用1000元再购进一批文学书和科普书,问购进文学书55本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
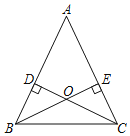
【题目】如图,锐角三角形ABC的两条高线BE、CD相交于点O,BE=CD.
(1)求证:BD=CE;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题探究)小敏在学习了Rt△ABC的性质定理后,继续进行研究.
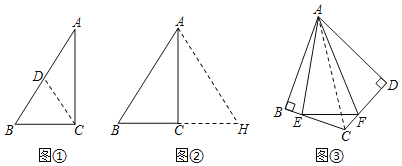
(1)(i)她发现图①中,如果∠A=30°,BC与AB存在特殊的数量关系是 ;
(ii)她将△ABC沿AC所在的直线翻折得△AHC,如图②,此时她证明了BC和AB的关系;请根据小敏证明的思路,补全探究的证明过程;
猜想:如果∠A=30°,BC与AB存在特殊的数量关系是 ;
证明:△ABC沿AC所在的直线翻折得△AHC,
(2)如图③,点E、F分别在四边形ABCD的边BC、CD上,且∠B=∠D=90°,连接AE、AF、EF,将△ABE、△ADF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形,连接AC,若∠EAF=30°,AB2=27,则△CEF的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款智能清洁机器人进行销售,很快销售一空,商家又用
元购进某款智能清洁机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款智能清洁机器人,所购进数量是第一次的
元第二次购进同款智能清洁机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进智能清洁机器人多少台?
(2)若所有智能清洁机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() (不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
(不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
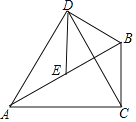
(1)求证:△ADE≌△CDB;
(2)若BC=1,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com