
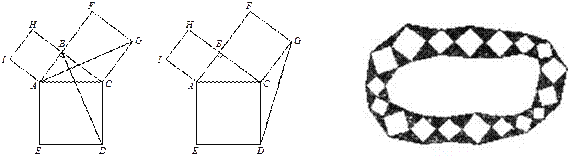
【题目】如图,在△ABC中,∠ABC=90°,分别以边AB、BC、CA向△ABC外作正方形ABHI、正方形BCGF、正方形CAED,连接GD,AG,BD. (提示:正方形的四条边相等,四个角均为直角,可直接运用。)
(1)如图1,求证:AG=BD.
(2)如图2,试说明:S△ABC=S△CDG.
(3)园林小路,曲径通幽,如图3所示,小路由白色的正方形大理石和黑色的三角形大理石铺成,已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地 平方米.(不用写过程)
【答案】(1)见解析;(2)见解析;(3)a+2b
【解析】试题分析:(1)由正方形的性质就可以得出△ACG≌△DCB,就可以得出结论;
(2)延长DC交GF于H,证明△BMC≌△GNC,就可以得出BM=GN,就可以得出结论.
(3)同(2)道理知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,求出这条小路一共占地多少平方米.
试题解析:(1)∵四边形ABHI、四边形BCGF和四边形CAED都是正方形,∴AB=BH=HI=AI,BC=CG=GF=BF,AE=DE=CD=AC,∠H=∠I=∠E=∠F=∠IAB=∠ABH=∠FBC=∠BCG=∠FGC=∠BAC=∠ACD=90°.
∴∠ACD+∠ACB=∠BCG+∠ACB,
∴∠DCB=∠ACG.
在△ACG和△DCB中,
 ,
,
∴△ACG≌△DCB(SAS),
∴AG=BD;
(2)如图,作BM⊥AC于M,GN⊥DC的延长于点N.

∴∠BMC=∠N=90°
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3.
在△BMC和△GNC中,
 ,
,
∴△BMC≌△GNC(AAS),
∴BM=GN,
∴![]() ACBM=
ACBM=![]() DCGN,
DCGN,
∵S△ABC=![]() ACBM,S△DCG=
ACBM,S△DCG=![]() DCGN,
DCGN,
∴S△ABC=S△CDG.
(3)由(2)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和。
∴这条小路的面积为(a+2b)平方米。


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】某市出租车收费标准是:起步价为8元,3千米后每千米为2元,若某人乘坐了x(x>5)千米.
(1)用含x的代数式表示他应支付的车费.
(2)行驶30千米,应付多少钱?
(3)若他支付了46元,你能算出他乘坐的路程吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图象如图1中的点状图所示(5月及以后每月的销售额都相同),而经销成本p(万元)与销售额y(万元)之间函数关系的图象图2中线段AB所示.

(1)求经销成本p(万元)与销售额y(万元)之间的函数关系式;
(2)分别求该公司3月,4月的利润;
(3)问:把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额﹣经销成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年12月13日,嫦娥二号成功飞抵距地球约700万公里远的深空,7 000 000用科学记数法表示为( )
A.7×105
B.7×106
C.70×106
D.7×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com