
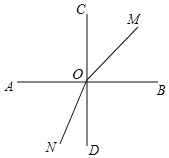
【题目】如图,两条直线AB、CD相交于点O,且![]() ,射线OM从OB开始绕O点逆时针方向旋转,速度为
,射线OM从OB开始绕O点逆时针方向旋转,速度为![]() ,射线ON同时从OD开始绕O点顺时针方向旋转,速度为
,射线ON同时从OD开始绕O点顺时针方向旋转,速度为![]() 两条射线OM、ON同时运动,运动时间为t秒
两条射线OM、ON同时运动,运动时间为t秒![]() 本题出现的角均小于平角
本题出现的角均小于平角![]()

![]() 当
当![]() 时,
时,![]() 的度数为多少,
的度数为多少,![]() 的度数为多少;
的度数为多少;![]() 的度数为多少;
的度数为多少;
![]() 当
当![]() 时,若
时,若![]() ,试求出t的值;
,试求出t的值;
![]() 当
当![]() 时,探究
时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)t的值为
;(2)t的值为![]() 秒或10秒;(3)当
秒或10秒;(3)当![]() 时,
时,![]() 的值不是定值;当
的值不是定值;当![]() 时,
时,![]() 的值是3.
的值是3.
【解析】
(1)根据时间和速度分别计算∠BOM和∠DON的度数,再根据角的和与差可得结论;
(2)分两种情况:①如图所示,当![]() 时,②如图所示,当
时,②如图所示,当![]() 时,分别根据已知条件列等式可得t的值;
时,分别根据已知条件列等式可得t的值;
(3)分两种情况,分别计算![]() 、
、![]() 和
和![]() 的度数,然后代入可得结论.
的度数,然后代入可得结论.
![]() 由题意得:
由题意得:![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ;
;
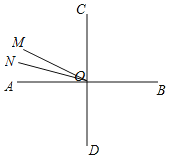
![]() 当ON与OA重合时,
当ON与OA重合时,![]()
当OM与OA重合时,![]()
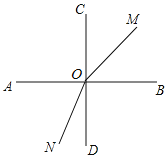
![]() 如图所示,当
如图所示,当![]() 时,
时,![]() ,
,![]()
由![]() ,可得
,可得![]() ,
,
解得![]() ,
,
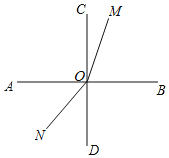
![]() 如图所示,当
如图所示,当![]() 时,
时,![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
综上,t的值为![]() 秒或10秒;
秒或10秒;
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 如图所示,当
如图所示,当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() 不是定值
不是定值![]() ,
,
![]() 如图所示,当
如图所示,当![]() 时,
时,![]() ,
,![]() ,
,
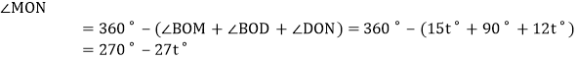 ,
,
![]() 定值
定值![]() ,
,
综上所述,当![]() 时,
时,![]() 的值不是定值;当
的值不是定值;当![]() 时,
时,![]() 的值是3.
的值是3.


科目:初中数学 来源: 题型:
【题目】问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1 ,P2 .
探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为 .
拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(5,3)、B(5,1). 
(1)在图中标出△ABC外心D的位置,并直接写出它的坐标;
(2)判断△ABC的外接圆D与x轴、y轴的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)求二次函数解析式及顶点坐标;
(2)点P为线段BD上一点,若S△BCP= ![]() ,求点P的坐标;
,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别为![]() ,4,点P为数轴上一动点,其对应的数为x
,4,点P为数轴上一动点,其对应的数为x
![]() 若点P到点A、点B的距离相等,求点P对应的数
若点P到点A、点B的距离相等,求点P对应的数
![]() 数轴上是否存在点P,使点P到点A、点B的距离之和为7?若存在,请直接写出x的值
数轴上是否存在点P,使点P到点A、点B的距离之和为7?若存在,请直接写出x的值![]() 若不存在,请说明理由?
若不存在,请说明理由?
![]() 若点P以1个单位
若点P以1个单位![]() 的速度从点O向右运动,同时点A以5个单位
的速度从点O向右运动,同时点A以5个单位![]() 的速度向左运动,点B以20个单位
的速度向左运动,点B以20个单位![]() 的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:
的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
根据城市规划设计,某市工程队准备为该城市修建一条长4800米的公路.铺设600m后,为了尽量减少施工对城市交通造成的影响,该工程队增加人力,实际每天修建公路的长度是原计划的2倍,结果9天完成任务,该工程队原计划每天铺设公路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com