
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:点B1的坐标为______;线段A1A2的长为______;△An-1BnAn的面积为______.

【答案】(1,1); 4; n2
【解析】
作B1C⊥y轴于C,B2D⊥y轴于D,如图,设OC=a,根据等腰直角三角形的性质得到OC=A1C=CB1=a,则B1(a,a),再把B1(a,a),代入y=x2得a1=0 (舍去),a2=1,所以B1(1,1),同理可得B2(2,4),则线段A1A2长为4,利用上述规律得到An1An=2n,然后根据等腰直角三角形的面积公式计算△An-1BnAn的面积即可.
解:作B1C⊥y轴于C,B2D⊥y轴于D,如图,设OC=a,

∵△OB1A1为等腰直角三角形,
∴OC=A1C=CB1=a,
∴B1(a,a),
把B1(a,a)代入y=x2得a2=a,解得a1=0(舍去),a2=1,
∴B1(1,1),
设A1D=b,
∵△A1B2A2为等腰直角三角形,
∴A1D=A2D=DB2=b,
∴B2(b,b+2),
把B2(b,b+2)代入y=x2得b2=b+2,解得b1=-1(舍去),b2=2,
∴B2(2,4),
∴线段A1A2的长为4,
同理可得A2A3=6,An-1An=2n,
∴△An-1BnAn的面积=![]() 2nn=n2.
2nn=n2.
故答案为(1,1);4;n2.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
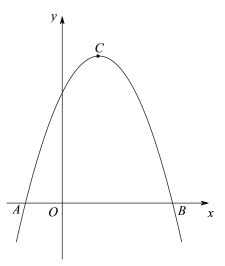
【题目】如图,在平面直角坐标系xOy中,二次函数![]() (a、b都是常数,且a<0)的图像与x轴交于点
(a、b都是常数,且a<0)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的解析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当∠PBA=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初三进入中考复习阶段以来,为了了解同学们晚上的睡眠情况,现对年级部分同学进行了调查统计,并制成如下两幅不完整的统计图:A代表睡眠时间4小时,B代表睡眠时间5小时,C代表睡眠时间6小时,D代表睡眠时间7小时,E代表睡眠时间8小时及以上,其中扇形统计图中“E”的圆心角为72°,请你结合统计图所给信息解答下列问题:
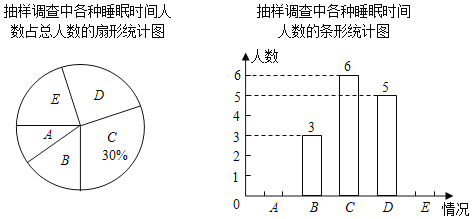
(1)共抽取了 名同学进行调查,同学们的睡眠时间的中位数是 小时左右,井将条形统计图补充完整;
(2)如果把睡眠时间低于7小时称为严重睡眠不足,请估算全校600个初三同学中睡眠严重不足的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD(AD>AB)中,P为BC边上的一点,AP=AD,过点P作PE⊥PA交CD于E,连接AE并延长交BC的延长线于F.
(1)求证:△APE≌△ADE;
(2)若AB=3,CP=1,试求BP,CF的长;
(3)在(2)的条件下,连结PD,若点M为AP上的动点,N为AD延长线上的动点,且PM=DN,连结MN交PD于G,作MH⊥PD,垂足为H,试问当M、N在移动过程中,线段GH的长度是否发生变化?若变化,请说明理由,若不变,求出GH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:
(1)如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EF GH;(填“>”“=”或“<”)
(2)如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证:![]() =
=![]() ;
;
(3)如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为底边分别作等腰三角形ABE和等腰三角形ADF.
(1)当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABE和等腰直角△ADF,连接BF、ED,线段BF和ED的数量关系是_____________;
(2)当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABE和等腰直角△ADF,连接EF、BD,线段EF和BD具有怎样的数量关系?请说明理由;
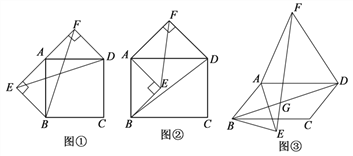
(3)当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABE和等腰△ADF,且△ABE和△ADF的顶角均为![]() ,连接EF、BD,交点为G.请用
,连接EF、BD,交点为G.请用![]() 表示出∠FGD,并说明理由.
表示出∠FGD,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=﹣x+7a+1与直线y=2x﹣2a+4同时经过点P,点Q是以M(0,﹣1)为圆心,MO为半径的圆上的一个动点,则线段PQ的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)已知CD=4cm,求AC的长;
(2)求证:AB=AC+CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com