
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是圆上不与点
是圆上不与点![]() 重合的动点,连接
重合的动点,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:![]() ;
;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当四边形![]() 是正方形时,
是正方形时, ![]() ________°
________°

【答案】(1)见解析;(2)①5,②45°
【解析】
(1)连接PB,利用直径所对的圆周角是直角,易得PB垂直平分AD,从而得到BA=BD,即可得证;
(2)①根据P为AD中点,C为BD中点,可得PC∥OA,PC=![]() AB=OA,从而判定四边形AOCP为平行四边形,再根据邻边相等的平行四边形为菱形即可的答案;
AB=OA,从而判定四边形AOCP为平行四边形,再根据邻边相等的平行四边形为菱形即可的答案;
②由正方形的性质可得∠POB=∠POA=90°,易得△OPA为等腰直角三角形,再利用PC∥AO即可得∠DPC=∠A=45°.
(1)证明:如图,连接![]()
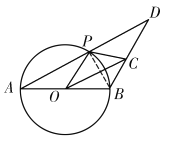
∵![]() 是
是![]() 的直径,
的直径,
![]()
![]() ,
,
![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]()
(2)①![]() ,
,
![]()
∵![]() 是
是![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
∴四边形![]() 是平行四边形
是平行四边形
∴当![]() 时,平行四边形
时,平行四边形![]() 是菱形.
是菱形.
故答案为:5.
②∵四边形![]() 是正方形,
是正方形,
∴∠POB=∠POA=90°
∵![]()
![]()
∴![]()
![]()
故答案为:45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形![]() 中,
中,![]() 于
于![]() ,
,![]() 平分
平分![]() 交线段
交线段![]() 于
于![]() .
.
(1)如果![]() ,求证:
,求证:![]() ;
;
(2)一般的情况下,如果![]() ,试探究线段
,试探究线段![]() 、
、![]() 与
与![]() 之间的所满足的等量关系(其中
之间的所满足的等量关系(其中![]() ,
,![]() 是已知数).
是已知数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在![]() 中,
中,![]() 90°,点
90°,点![]() 为
为![]() 的中点,以
的中点,以![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 恰好与点
恰好与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(2)在(1)的条件下,如果正方形![]() 绕点
绕点![]() 旋转,连接
旋转,连接![]() ,
,
①线段![]() 与
与![]() 的数量关系有无变化?请仅就图2的情形给出证明;
的数量关系有无变化?请仅就图2的情形给出证明;
②当正方形![]() 旋转到
旋转到![]() 三点共线时,直接写出线段
三点共线时,直接写出线段![]() 的长.
的长.
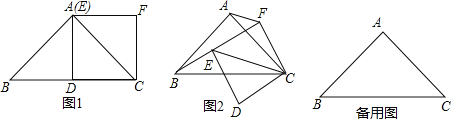
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() .经试销发现,销售量
.经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数关系,当销售单价为
(元)符合一次函数关系,当销售单价为![]() 元时销售量为
元时销售量为![]() 件,当销售单价为
件,当销售单价为![]() 元时销售量为
元时销售量为![]() 件.
件.
(1)此试销期间销售量![]() 可能为
可能为![]() 吗?说明理由.
吗?说明理由.
(2)销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒令是中国民间风俗之一.白居易曾诗曰:“花时同醉破春愁,醉折花枝当酒筹”饮酒行令,是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜迷形拳之举,最早诞生于西周,完备于隋唐,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时或喊虎、喊棒、喊鸡、喊虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒兴鸡、或虫兴虎同时出现(解释:若棒与鸡,虎与虫同时喊出)或两人喊出同一物,则不分胜负,继续喊”.依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)用列表法或画树状图法,求李四取胜的概率;
(3)直接写出两人能分出胜负的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象交于坐标轴上的
的图象交于坐标轴上的![]() 两点.
两点.
(1)求二次函数的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一点,过点
上方抛物线上一点,过点![]() 分别作
分别作![]() 轴
轴![]() 轴平行线分别交直线
轴平行线分别交直线![]() 于点
于点![]() 和点
和点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的周长,并求出当
的周长,并求出当![]() 的周长取得最大值(不需要求出此最大值)时点
的周长取得最大值(不需要求出此最大值)时点![]() 的坐标;
的坐标;
(3)点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是抛物线上一点,在第二问
是抛物线上一点,在第二问![]() 的周长取得最大值的条件下,请直接写出使以点
的周长取得最大值的条件下,请直接写出使以点![]() 为顶点的四边形是平行四边形的点
为顶点的四边形是平行四边形的点![]() 的坐标.
的坐标.
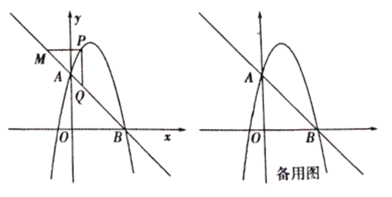
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 得到四边形
得到四边形![]() .点
.点![]() 在边
在边![]() 上,连接
上,连接![]() ,将边
,将边![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,若点
,若点![]() 到四边形
到四边形![]() 较长两对边的距离之比为
较长两对边的距离之比为![]() .则点
.则点![]() 的坐标为_______.
的坐标为_______.
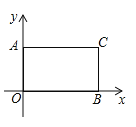
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com