
����Ŀ����֪һ�κ���y=��![]() x+
x+![]() ��ͼ����x�ᡢy��ֱ���A��B���㣮ֱ��l����A�Ҵ�ֱ��x�ᣮ������D��E�ֱ��A B�����ʱ������O���˶����˶���O��ֹͣ�����˶��ٶȷֱ���ÿ��1����λ���Ⱥ�
��ͼ����x�ᡢy��ֱ���A��B���㣮ֱ��l����A�Ҵ�ֱ��x�ᣮ������D��E�ֱ��A B�����ʱ������O���˶����˶���O��ֹͣ�����˶��ٶȷֱ���ÿ��1����λ���Ⱥ�![]() ����λ���ȣ���G��E����ֱ��l�Գƣ�GE��AB�ڵ�F����D��E���˶�ʱ��Ϊt��s����
����λ���ȣ���G��E����ֱ��l�Գƣ�GE��AB�ڵ�F����D��E���˶�ʱ��Ϊt��s����
��1����tΪ��ֵʱ���ı��������Σ��жϴ�ʱ��AFG��AGB�Ƿ����ƣ���˵�����ɣ�
��2������ADF��ֱ��������ʱ�����BEF���BFG�����֮�ȣ�

���𰸡�(1)������;(2)![]() .
.
��������
��1���������A��B�����꣬������ɵ�EF=t��BF=2t��AF=2��2t��AD=t���Ӷ��ı���ADEFΪƽ���ı��Σ���AD=AFʱ��![]() ADEF�����ο����t��ֵ������������Ǻ�����֪ʶ������EBG=60�㣬�Ӷ���ABG=30�㣬����������ȵ��������������ƿ�֤��AFG�ס�AGB��
ADEF�����ο����t��ֵ������������Ǻ�����֪ʶ������EBG=60�㣬�Ӷ���ABG=30�㣬����������ȵ��������������ƿ�֤��AFG�ס�AGB��
��2���֡�ADF=90��͡�AFD=90�����������⼴��.
�⣺��1����������ɵã�A��1��0����B��0��![]() ������OBA=30�㣬
������OBA=30�㣬
��BE=![]() t��
t��
��EF=t��BF=2t��AF=2��2t��
��AD=t��
��EF=AD����EF��AD��
���ı���ADEFΪƽ���ı��Σ�
��AD=AFʱ��ADEF�����Σ�����t=2��2t�����t=![]() ��
��
�ڴ�ʱ��AFG���AGB���ƣ��������£�
���ͼ1��ʾ������AE����AE=AG��

���AGE=��AEG=30�㣮
��Rt��BEG��BE=![]() ��EG=2��
��EG=2��
��tan��EBG=![]() =
=![]() ��
��
���EBG=60�㣬
���ABG=��EBG����EBF=30�㣮
�ڡ�AFG���AGB�У��ߡ�BAG=��GAF����ABG=��AGF=30�㣬
���AFG�ס�AGB��
��2���ߡ�DAF=60�㣬
�൱��ADF=90��ʱ��AF=2AD������2��2t=2t�����t=![]() ��
��
��ʱEF=![]() ��FG=
��FG=![]() ��
��
��![]() =
=![]() =
=![]() ��
��
�൱��AFD=90��ʱ��AD=2AF������t=2��2��2t�������t=![]() ��
��
��ʱEF=![]() ��FG=
��FG=![]() ��
��
��![]() =
=![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ��Բ���ܵ���Բ���ܵ����ܳ�С��700m����һֱ������A��B�������ܣ���һ������ʱ��A��100m���ڶ�������ʱ��B��60m����Բ���ܵ����ܳ�Ϊ�� ��

A.240mB.360mC.480mD.600m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��OAB�Ķ���A��x����������ϣ�����B������Ϊ��3��![]() ������C������Ϊ��1��0�����ҡ�AOB=30����PΪб��OB�ϵ�һ�����㣬��PA+PC����СֵΪ���� ����
������C������Ϊ��1��0�����ҡ�AOB=30����PΪб��OB�ϵ�һ�����㣬��PA+PC����СֵΪ���� ����

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪m��n��m<n���ǹ���x�ķ��̣�x�Ca����x�Cb��=2����������a<b���������ж���ȷ����
A. a<m<b<n B. m<a<n<b
C. a<m<n<d D. m<a<b<n
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AB��AC��D��E�ǡ�ABC�����㣬ADƽ�֡�BAC����EBC����E��60������BE��10��DE��4����BC�ij�����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
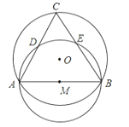
����Ŀ����ͼ����O�İ뾶Ϊ2����AB�ij�Ϊ2![]() ����ABΪֱ������M����C���Ż���AB�ϵ�һ�����㣬����AC��BC�ֱ���M�ڵ�D��E�����߶�CD�����ֵΪ��������
����ABΪֱ������M����C���Ż���AB�ϵ�һ�����㣬����AC��BC�ֱ���M�ڵ�D��E�����߶�CD�����ֵΪ��������
A. ![]() B. 2 C. 2
B. 2 C. 2![]() -2 D. 4-2
-2 D. 4-2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���ACB=90����AC=BC=4����DΪAB���е㣬M��N�ֱ���BC��AC�ϣ���BM=CN���������ĸ����ۣ�
��DN=DM�� �� ��NDM=90���� �� �ı���CMDN�����Ϊ4�� �ܡ�CMN��������Ϊ2.
������ȷ�Ľ����У� ��

A. �٢ڢ��� B. �٢ڢ��� C. �ڢۢ��� D. �٢ڢۢ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���г�Ϊ30����ʣ�Χ���м����һ����ʵij����εĻ��ԣ��һ��Եij��ɽ���һ��ǽ�壨ǽ�������ʹ�ó���a=10�ף����軨�Ե�һ��AB��Ϊx�ף����Ϊyƽ���ף�
��1����y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
��2�������Χ�ɵĻ��Ե����Ϊ63ƽ���ף������AB�ij���
��3������Ŀ�����Ҫ���� ������������������������Χ�����Ϊ80ƽ���Ļ��ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У���A��B�ĺ�����ֱ�Ϊa��a+2�����κ���y=��x2+��m��2��x+2m��ͼ����A��B����a��m����2a��m=d��dΪ��������
��1����һ�κ���y1=kx+b��ͼ��A��B���㣮
�ٵ�a=1��d=��1ʱ����k��ֵ��
����y��x���������С����d��ȡֵ��Χ��
��2����d=��4��a����2��a����4ʱ���ж�ֱ��AB��x���λ�ù�ϵ����˵�����ɣ�
��3����A��B��λ������a�ı仯���仯�����A��B�˶���·����y��ֱ��ཻ�ڵ�C��D���߶�CD�ij��Ȼᷢ���仯��������䣬���CD�ij�������仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com